Задания на расчётно-графические работы по дисциплине «Математическое моделирование физических процессов», страница 2

Задание 13. Моделирование нелинейного маятника.

            Для нелинейного маятника промоделируйте вынужденные колебания с периодической вынуждающей силой при следующих условиях: w₀² = g/L=9[c^-2]; коэффициент затухания g = 0.5, частота вынуждающей силы w=2c^-1. Начальное смещение и начальная скорость равны нулю. Определить зависимость амплитуды установившихся колебаний от амплитуды вынуждающей силы при f₀ = F/m = 0.5; 1; 2; 4[кг/с²]. Построить зависимость А(f₀). Объяснить результаты.

Задание 14. Моделирование колебаний под  действием вынуждающей силы.

            Для вынужденных колебаний с собственной частотой w₀ = 3с^-1 и коэффициентом затухания g =0.5 получите зависимость х₁(t) для внешней гармонической силы F₁(t) = cos wt, затем х₂(t) для силы F₂(t) = 2 cos wt, а затем зависимость х₃(t) для силы F₃(t) = F₁(t) + F₂(t). Проанализируйте результаты.

Начальные значения смещения и скорости можно положить равными нулю.

Частота вынуждающей силы w = 2с^-1.

Задание 15. Моделирование ядерной цепной реакции деления.

Постановка задачи. Ядерная реакция, при которой частицы, вступающие в реакцию, образуются и в результате реакции, называется цепной ядерной реакцией. Типичным примером является цепная реакция деления ядер ²³⁵U  под действием нейтронов:

                                 n + ²³⁵U → A + B + υn,

где n – нейтрон, A, B – осколки деления, υ>2. Образовавшиеся в результате деления (вторичные) нейтроны вызовут деления в других ядрах  ²³⁵U, т.е. реакция приобретает цепной характер. От скорости образования вторичных нейтронов зависит характер энерговыделения: будет ли это ядерный взрыв или регулируемая стационарная реакция, которая используется в ядерных  реакторах на АЭС или в двигателях на атомных ледоколах и подводных лодках.

            Самой важной характеристикой конкретного реактора является коэффициент размножения нейтронов k, равный отношению полного числа вторичных нейтронов в последующем поколении к числу нейтронов в предыдущем поколении. Если в первом поколении было N нейтронов, то в

 n+1-м поколении их будет N*kⁿ. Процесс вылета нейтронов при делении ядра практически мгновенный – за 10^-12 – 10^-14 с. Эти нейтроны называют мгновенными. Смена поколений мгновенных нейтронов происходит очень быстро – за время Т ~ 10^-4 – 10^-6 с, т.е. среднее время жизни мгновенных  нейтронов Т очень мало. Значит за 1 с сменится порядка n = 10⁴ – 10⁶ поколений нейтронов, и число нейтронов возрастет в kⁿ раз. Если k даже совсем мало отличается от 1 (k=1+10^-3), число нейтронов возрастает очень быстро, и управлять реакцией на одних мгновенных нейтронах невозможно.

            Однако при дальнейших радиоактивных распадах некоторых (нейтронно-активных) осколков также вылетают нейтроны, которые называют запаздывающими. Они появляются через несколько секунд после вылета мгновенных нейтронов, и время их жизни, которое определяется средним временем жизни нейтронно-активных осколков по отношению к испусканию нейтрона, составляет десятки секунд (Т_зап ~ 10–60 с). Доля β запаздывающих нейтронов в общем количестве вторичных нейтронов невелика: β ~(0.2-0.7)10^-2, тем не менее, именно наличие этих нейтронов дает возможность регулирования реакции деления. 

            С учетом запаздывающих нейтронов коэффициент размножения нейтронов k можно представить в виде суммы коэффициентов размножения на мгновенных и запаздывающих нейтронах: k= k_мг+ k_зап, причем k_мг=(1- β) k,

k_зап= β k. Система уравнений, описывающая изменение числа вторичных нейтронов N, которое зависит также от изменения количества С нейтронно-активных осколков, записывается в следующем виде:

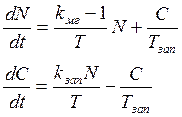
Здесь Т, Т_зап – средние времена жизни мгновенных и запаздывающих нейтронов соответственно, начальное значение N можно взять произвольным (10, 100), начальное значение С можно положить равным нулю или 1. Эта система получена в предположении .

            Задача заключается  в исследовании закономерностей изменения  N(t), C(t) в зависимости от параметров Т, Т_зап, β, k. Примерные интервалы значений первых трех параметров приведены выше. Выражение для  k удобно взять в виде k=1+δ и рассмотреть случаи k= β,  k< β,   k<<β. (На практике малое отличие k от 1 достигается введением в зону реакции поглотителей нейтронов).

Задание  Провести исследование решения заданной системы уравнений и при

выбранных значениях Т, Т_зап, β определить области k, в которых интенсивность ядерной реакции деления растет, падает или поддерживается на постоянном уровне.

Задание 16.  Моделирование скорости химической реакции.

Постановка задачи. Одностадийная обратимая реакция типа А↔В описывается системой дифференциальных уравнений

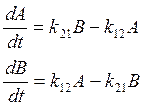            А_t=0=1,  B_t=0=0.

Здесь А, В  - относительные концентрации реагирующих компонент; k_12, k₂₁ ­– константы скоростей реакции.

            Построить зависимости изменения концентраций во времени A(t), B(t) для трех вариантов:

№ варианта	k12,	k21
1	1	0.05
2	1	0.5
3	0.05	0.25

Описать алгоритм численного решения, программу. Провести анализ результатов.

Задание 17  Моделирование изменения атмосферного давления с ростом расстояния от поверхности Земли.

Постановка задачи. Примем следующие предположения для математической модели : 1) температура воздуха не зависит от высоты над поверхностью; 2) воздух является идеальным газом; 3) гравитационные силы подчиняются закону Ньютона. Тогда можно показать, что давление Р на расстоянии х от центра Земли удовлетворяет уравнению:

    (1), причем на поверхности Земли (х=R) P(R)=1атм.

Здесь R – радиус Земли, K_p=kM/cg (k – гравитационная постоянная, М – масса Земли, g – ускорение свободного падения, с – константа). Если эти параметры выбраны в одной и той же системе единиц, отношение K_p/R=0.9.

Уравнение (1) удобно привести к безразмерному виду. Для этого введем новые переменные: x=h+R, z=h/R, P(x)=P(R(1+z))=y(z). Так как z<<1, то пренебрегая величиной z², уравнение (1) сведем к виду:

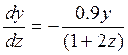   (2) (попробуйте провести эти преобразования самостоятельно). Начальное условие, которое обеспечивает единственность решения, формулируется как у(0)=1 (3).

Уравнение (2) с условием (3) – типичная постановка задачи Коши.

Аналитическое решение этой задачи дает следующие результаты:

z	0	0.02	0.04	0.06	0.08	0.1	0.2
y(z)	1	0.9825	0.9660	0.9503	0.9354	0.9213	0.8610

1. Получите численное решение, используя метод Эйлера.

2. Постройте зависимость y(z).

3. Опишите алгоритм и программу вычислений.

4. Сделайте выводы относительно погрешности численного метода для данной задачи.