





С целью устранения недостатков, свойственных методу расчета сечений проводов по табличной нормированной экономической плотности тока, в 1945 г. В.М. Блок была предложена методика* определения экономических сечений проводов путем построения экономических интервалов.
Определение экономических интервалов нагрузки состоит в следующем.
Приведенные затраты линии электропередачи заданного типа, напряжения и сечения проводов на единицу ее длины представляются в виде выражения
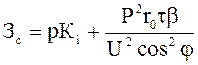 . (9.71)
. (9.71)
Это выражение, рассматриваемое как Зi = f(P), представляет параболу вида Зi = a + bP2.
Для каждого стандартного сечения линии данного типа и напряжения могут быть рассчитаны и построены в координатах Зi и P соответствующие параболы (рис. 9.8). Точки пересечения этих парабол определяют границы и интервалы мощности, в которых применение стандартных сечений является экономичным, так как соответствуют наименьшим значениям приведенных затрат. Экономический интервал мощности для провода сечением Fi ограничивается точками пересечения “a” и “б” параболы, соответствующей этому сечению с параболами, соответствующими соседним значениям Fi-1 и Fi+1 в ряду стандартных сечений (см. рис. 9.8).
Метод экономических интервалов характерен определением граничной нагрузки, при превышении которой экономически целесообразно переходить на большее сечение. Эта граничная нагрузка Рг определяется уравнением
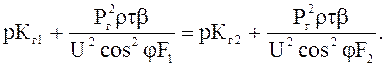
Отсюда находится граничная нагрузка
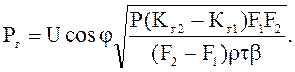 (9.72)
(9.72)
Аналогично находятся точки Рг2, Рг3, …, при попарном сравнении сечений F2 и F3 > F2; F3 и F4 > F3 и т.д.
Этот метод имеет недостаток, свойственный предыдущему методу табличной нормированной экономической плотности тока. Действительно в формуле (9.72) величины Кг1 и Кг2 отражают капитальные затраты при любой зависимости от сечения проводов. В них всегда содержится постоянная часть, которая в данном выражении пропадает. В результате получается заниженное значение Рг, а в случае с ЛЭП на унифицированных опорах, когда Кг1 » Кг2 [24] нагрузка Рг становится равной или близкой к нулю, что не соответствует реальной экономичности.
C целью устранения этого недостатка следует граничные нагрузки определять как экономические, соответствующие минимальной стоимости передачи электроэнергии. Такая экономическая нагрузка соответствует рассмотренным ранее в параграфе 9.2 экономическому КПД и экономической мощности.
На рис. 9.9. изображены несколько проводников со стандартными сечениями F1, F2, F3 … и их экономическими нагрузками Рэ1, Рэ2, Рэ3 … . Показаны также заданные нагрузки Р1, Р2, Р3…
Если заданная нагрузка равна экономической мощности
Pэ1, то наиболее экономичным будет сечение F1. Если заданная нагрузка Р2 = Рэ2,
то наиболее экономичным будет сечение F2 и
т.д. В тех случаях, когда заданная нагрузка ![]() отклоняется от экономической Рэ1
до определенного граничного значения Рг1, наиболее экономичным
остается проводник с сечением F1. Если же
заданная нагрузка
отклоняется от экономической Рэ1
до определенного граничного значения Рг1, наиболее экономичным
остается проводник с сечением F1. Если же
заданная нагрузка ![]() оказывается больше
граничной нагрузки Рг1, приближаясь к экономической мощности Рэ2,
то наиболее экономичным становится сечение F2
> F1. Граничная нагрузка для проводника с
меньшим сечением определяется как среднее геометрическое значение двух
экономических мощностей для смежных по шкале сечений
оказывается больше
граничной нагрузки Рг1, приближаясь к экономической мощности Рэ2,
то наиболее экономичным становится сечение F2
> F1. Граничная нагрузка для проводника с
меньшим сечением определяется как среднее геометрическое значение двух
экономических мощностей для смежных по шкале сечений
![]()
Покажем, что это действительно так.
Для экономической мощности в параграфе 9.2 получена формула
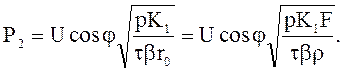 (9.73)
(9.73)
Представим, что искомая граничная мощность Рг является экономической для проводника с промежуточным сечением Fг, тогда согласно (9.73)
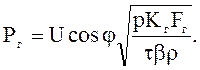
Стоимости передачи электроэнергии для провода сечением Fг при экономических мощностях Рэ1 и Рэ2 будут
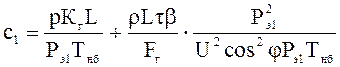
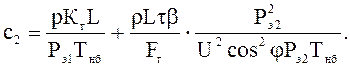
Приравнивая с1 и с2, получим уравнение
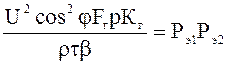 или
или
![]()
Отсюда искомая формула
![]() (9.74)
(9.74)
Экономические мощности для сечений F2 и F2, согласно (9.72) будут равны
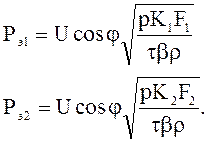
Подставляя эти значения в формулу (9.74), получим
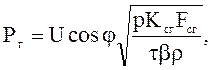 где Ксг и Fсг – среднегеометрические
значения К1 и К2, F1 и
F2:
где Ксг и Fсг – среднегеометрические
значения К1 и К2, F1 и
F2:
![]()
Таким образом, если сравниваются два проводника с разными сечениями F1 и F2 > F1, то при заданной нагрузке Р < Рг1, наиболее экономичным оказывается проводник с меньшим сечением F1, а при нагрузке Р > Рг1 – экономичнее проводник сечением F2.
Аналогично определяются граничные нагрузки Рг2, Р3 … и находятся экономические сечения проводов.
Описанная методика представляется сравнительно простой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.