Совместный выбор напряжения линии и ее сечения. Расчет характерных режимов электрических сетей, страница 2

Граничная длина определяется равенством

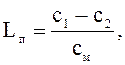где

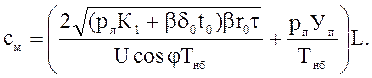
Сочетание экономических интервалов (рис.9.11), длины L_0,9 и граничной длины всех СРП образует зону оптимизации электропередачи (рис. 9.12).

У каждой СРП есть своя экономическая область, которая образуется интервалами экономических мощностей и граничной длиной.

На рис. 9.12 приведены экономические области всех СРП. Слева от линии L_0,9 находятся экономические области всех СРП с h ³ 0,9, а справа ‑ h < 0,9.

При прохождении по проводу электрического тока провод нагревается. Температура провода постепенно повышается, пока не установится равновесие между количеством тепла, сообщаемого током проводу и количеством тепла, которое передается окружающей среде.

Пусть С ‑ теплоемкость провода, равная произведению веса (или массы) провода на его удельную теплоемкость*; Т. Т_у,  ‑ разности промежуточной и конечной установившейся температуры провода по отношению к температуре окружающей среды; F_o ‑ охлаждающая поверхность провода; a ‑ коэффициент теплоотдачи ‑ согласно закону Ньютона, отдаваемая в единицувремени теплота пропорциональна разности температур Т проводника и окружающей среды и величине охлаждающей поверхности проводника**; t ‑ время от начала включения тока.

Сообщаемая проводнику за время dt теплота Рdt = I²Rdt будет уходить частью (равной CdT) на повышение температуры провода, а в остальной части (равной aF_oTdt), будет отдаваться внешней среде, т.е.

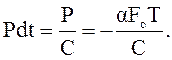
или

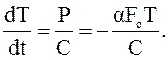
Температура установившегося режима будет :

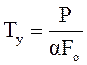
и

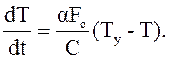
Разделяя переменные, получим:

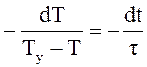, где 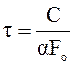 ‑ носит название постоянной времени.

Решение этого дифференциального уравнения дает:

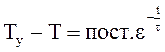
При t = 0 находим пост.=Т_у.

Превышение температуры провода над температурой окружающей среды представится:

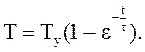
Эта зависимость, выражающая закон нагревания провода, представлена на рис. 9.13 графически (кривая А).

Постоянная времени представляет собой время, в течение которого провод получил бы ту же температуру перегрева Т_у, если бы не было отдачи тепла в окружающую среду. Это видно из равенства:

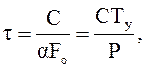
где СT_y ‑ количество тепла, потребное для повышения температуры провода доТ_у при условии отсутствия отдачи тепла;

Р ‑ количество тепла, выделяемое при прохождении тока в единицу времени.

Если после достижения проводом определенной температуры выключить ток, то провод будет охлаждаться; отдаваемое в единицу времени во внешнюю среду тепло равно уменьшению теплосодержания в единицу времени:

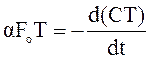или

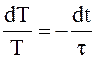
отсюда

Приt = 0T = To, следовательно

.

Эта формула, выражающая закон охлаждения провода, также представлена графически на рис. 9.13 (кривая Б).

Если электрический ток проходит по проводнику с перерывами, тогда кривая изменения температуря изобразится ломаной линией В (см. рис. 9.13)

При прерывистой нагрузке температура провода будет значительно ниже максимальной конечной температуры провода при том же токе постоянной величины. Поэтому при прерывистой нагрузке могут допускаться большие токи, чем при постоянной нагрузке.

Из изложенного можно сделать также вывод, что заданному длительно протекающему по проводу току при определенных условиях охлаждения соответствует вполне определенное превышение температуры провода над температурой окружающей среды и обратно – данному перепаду температуры соответствует вполне определенный длительно протекающий ток.

Целью расчетов проводов и кабелей на нагрев является определение допустимого тока для заданного перепада температур.

Эти расчеты служат для предупреждения опасного перегрева проводов и кабелей.

9.14. Выбор сечений проводов воздушных линий по условию короны

Провода ВЛ по условию короны должны удовлетворять условию:

                                           Е_макс £ 0,9Е₀,                                       (9.56) где Е_макс – наибольшая напряженность электрического поля у поверхности любого провода при среднем эксплуатационном напряжении;

Е₀ – напряженность электрического поля, соответствующая появлению общей короны.