Исследование электростатического поля двухпроводной линии (Лабораторная работа № 31)

Л а б о р а т о р н а я   р а б о т а   №31

ИССЛЕДОВАНИЕ электростатического поля

двухпроводной линии

31.1. Цель работы

1. Изучение методов расчета параметров электростатического поля двухпроводной линии в произвольной точке пространства.

2. Исследование электростатического поля двухпроводной линии методом математического моделирования на ЭВМ.

31.2. Исходные данные

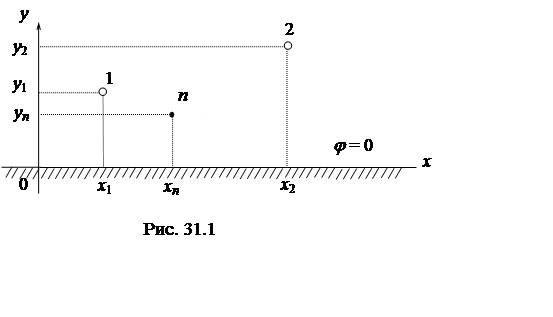
Два провода 1 и 2 радиусом R=3 мм расположены параллельно над проводящей плоскостью («землей») (рис. 31.1). Провода находятся под потенциалами  j₁ и  j₂ по отношению к «земле», потенциал которой равен нулю. Пространственные координаты проводов (x₁, y₁ , x₂, y₂ ) в плоскости x – y поперечного сечения линии и их потенциалы (j₁,j₂) заданы в табл. 31.1. Заданы координаты двух расчетных точек n₁ и n₂: (x_n1=60 см, y_n1=30 см, x_n2=80 см, y_n2=80 см)

Т а б л и ц а  31.1

31.3. Теоретические сведения

Электростатическое поле в диэлектрической среде создается неподвижными в пространстве и постоянными во времени электрическими зарядами. Электрические заряды могут быть расположены в отдельных точках q (Кл), по поверхности проводящих тел с поверхностной плотностью s(Кл/м²), вдоль тонких проводов с линейной плотностью t (Кл/м), и по объему с объемной плотностью r(Кл/м³).

Электростатическое поле в произвольной точке n можно описать уравнениями электростатики в дифференциальной форме: 

 ,    ,     ,     ,     .

Для расчета простейших симметричных полей могут быть использованы те же уравнения, но в интегральной форме:

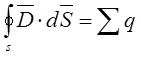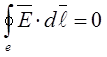 ,         ,             , где – вектор электрического смещения, Кл/м;

– вектор напряженности поля, В/м;

j– потенциал, B.

В решаемой задаче электростатическое поле создается линейными зарядами проводов t₁ и t₂ и поверхностными зарядами «земли» s_з, наведенными посредством электростатической индукции. Расчет параметров поля (j, ) от действия осевых зарядов t довольно прост, в то же время непосредственный учет поверхностных зарядов вызывает существенные осложнения.

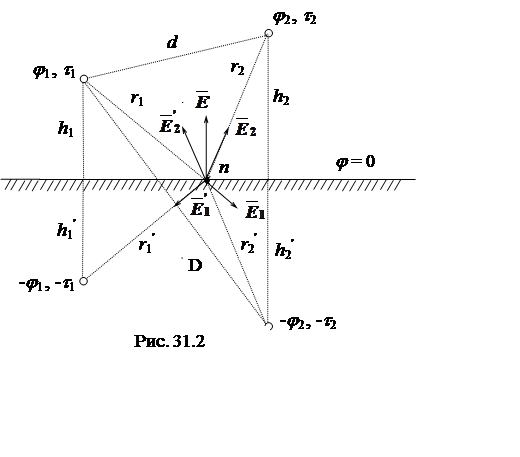
Задача по расчету поля от системы заряженных проводов с учетом «земли» решается методом зеркальных отображений. Сущность метода состоит в том, что поверхностные заряды «земли» s₃ заменяются осевыми зарядами –t₁ и –t₂ , расположенными зеркально заданным зарядам t₁ и t₂ (рис. 31.2). В соответствии с теорией в таком случае сохраняются неизменными граничные условия (Е_t = 0, j = 0) и, следовательно, электростатическое поле в верхней части полупространства не нарушается.

В данной задаче известными являются потенциалы проводов j₁ и j₂ и их геометрическое расположение.

Заряды проводов t₁ и t₂ определяются из системы потенциальных уравнений

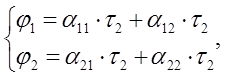
где потенциальные коэффициенты a выражаются через геометрические размеры:

  ;          ;          

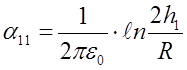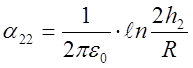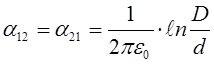
Составляющая вектора напряженности электростатического поля в произвольной точке n от отдельного осевого заряда t направлена по радиусу от провода (t> 0) или к проводу (t < 0), ее модуль определяется по формуле:

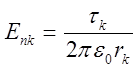, а составляющая  потенциала – 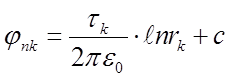   , где r_k – расстояние от точки n до провода, с – постоянная интегрирования.

Результирующий вектор напряженности электростатического поля  и результирующий потенциал j_n в произвольной точке n могут быть найдены по принципу наложения, как соответствующие суммы составляющих от отдельных проводов и их зеркальных отображений. Очевидно, что составляющие вектора  необходимо складывать векторно, а составляющие потенциала j_n – скалярно:

 ,

j_n= j_n1 + j_n2 + j¢_n1+ j¢_n2.

При векторном суммировании отдельные слагаемые раскладываются на составляющие по координатным осям x и y , затем находятся суммы составляющих по осям   и , через которые выражается результирующий вектор:

 ,      .

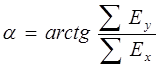Векторное суммирование отдельных слагаемых можно выполнить в комплексной форме (оси x соответствует ось вещественных величин +1, а оси y – ось мнимых величин +j):

 = SE_x + jSE_y = E_n e ^ja

Эквипотенциальными поверхностями называются воображаемые поверхности постоянного потенциала j_s = const. В плоскости сечения эквипотенциальные поверхности образуют следы – линии.