

















время остается меньше ЭДС ![]() вторичной обмотки
трансформатора из-за потерь напряжения на внутренних сопротивлениях
трансформатора и вентиля от зарядного тока.
вторичной обмотки
трансформатора из-за потерь напряжения на внутренних сопротивлениях
трансформатора и вентиля от зарядного тока.
В момент времени ![]() напряжение
на конденсаторе становится равным ЭДС вторичной обмотки, ток через вентиль
спадает до нуля. Заряд конденсатора прекращается, и начинается его разряд на
сопротивление нагрузки
напряжение
на конденсаторе становится равным ЭДС вторичной обмотки, ток через вентиль
спадает до нуля. Заряд конденсатора прекращается, и начинается его разряд на
сопротивление нагрузки ![]() (участок II на
рис. 2). Ток разряда конденсатора в сопротивлении
(участок II на
рис. 2). Ток разряда конденсатора в сопротивлении ![]() по
направлению совпадает с током нагрузки в момент времени
по
направлению совпадает с током нагрузки в момент времени ![]() ÷
÷![]() .
.
Напряжение на конденсаторе при разряде
спадает по экспоненциальной кривой, наклон которой, как будет показано в §2,
зависит от величины сопротивления нагрузки ![]() в емкости
конденсатора
в емкости
конденсатора ![]() .
.
Разряд конденсатора длится до тех пор, пока ЭДС вторичной обмотки трансформатора вновь не становится равной напряжению на конденсаторе. В следующие моменты времени ЭДС вторичной обмотки превышает напряжение на конденсаторе, и процесс заряда конденсатора повторяется.
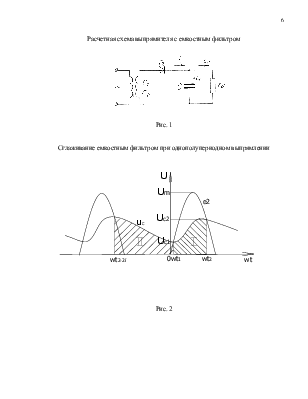
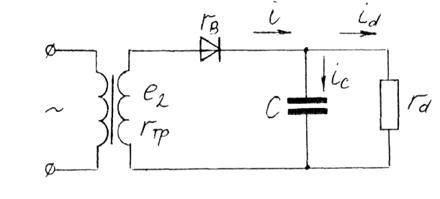
Расчетная схема выпрямителя с емкостным фильтром
 |
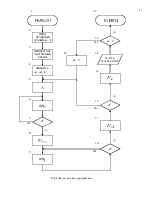
 Сглаживание емкостным фильтром при однополупериодном выпрямлении
Сглаживание емкостным фильтром при однополупериодном выпрямлении2.Расчет среднего значения выпрямленного сглаженного напряжения
Для упрощения расчета будем считать
внутреннее сопротивление вентиля ![]() постоянным, не
зависящим от тока, а сопротивление трансформатора, приведенного ко вторичной
обмотке, чисто активным:
постоянным, не
зависящим от тока, а сопротивление трансформатора, приведенного ко вторичной
обмотке, чисто активным:
![]() , где
, где ![]() и
и ![]() - активные сопротивления первичной и
вторичной обмоток трансформатора.
- активные сопротивления первичной и
вторичной обмоток трансформатора.
Сопротивление фазы выпрямителя равно сумме внутренних сопротивлений вентилей и трансформатора:
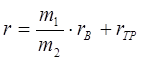 , где
, где ![]() - количество вентилей,
включенных последовательно (например, при мостовой схеме
- количество вентилей,
включенных последовательно (например, при мостовой схеме ![]() );
);
![]() -
количество вентилей, включенных параллельно.
-
количество вентилей, включенных параллельно.
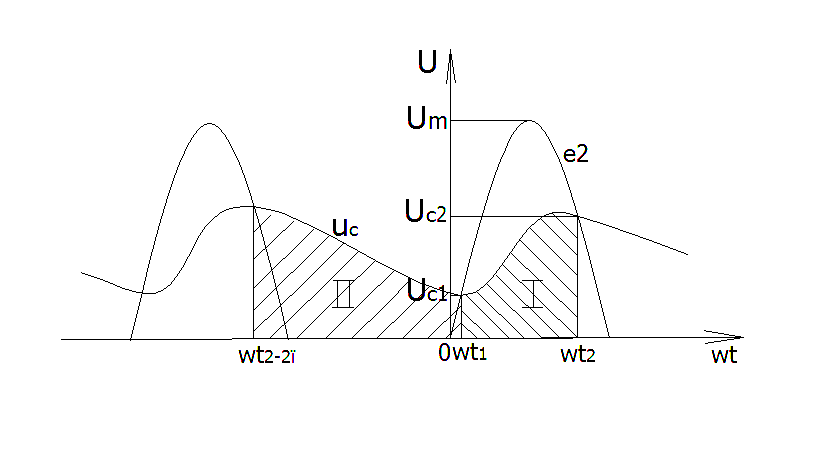
ЭДС вторичной обмотки трансформатора изменяется по синусоидальному закону (рис. 2)
![]() .
.
Проанализируем процесс заряда конденсатора (участок I рис.2)
Ток выпрямителя
![]() ,
(1)
,
(1)
где 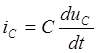 - ток через емкость;
- ток через емкость;
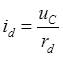 -
ток через нагрузку.
-
ток через нагрузку.
Напряжение на конденсаторе ( и на нагрузке)
![]() . (2)
. (2)
Подставим (1) в (2), получим
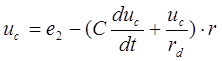
или
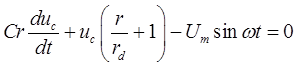 (3)
(3)
Найдем закон изменения ![]() , решив
дифференциальное уравнение (3):
, решив
дифференциальное уравнение (3):
![]() , (4)
, (4)
где ![]() ,
, ![]() - соответственно принужденная и свободная
составляющая напряжения на конденсаторе.
- соответственно принужденная и свободная
составляющая напряжения на конденсаторе.
Принужденная составляющая ![]()
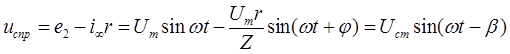 , (5)
, (5)
где 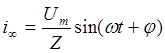 - ток установившегося
режима ( при
- ток установившегося
режима ( при ![]() );
);
![]() ;
; 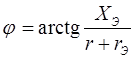 ;
; 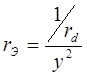 ;
; 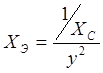 ; (5а)
; (5а)
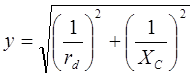 ;
; 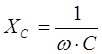 ;
;
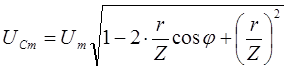 ;
; ![]()
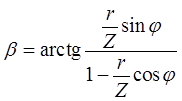 .
.
Свободная составляющая ![]() изменяется
по экспоненциальному закону
изменяется
по экспоненциальному закону
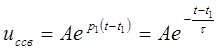 , (6)
, (6)
где ![]() - корень
характеристического уравнения, получаемого из (3):
- корень
характеристического уравнения, получаемого из (3):
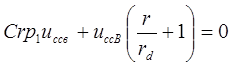 , откуда
, откуда
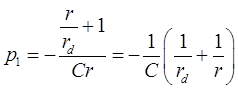 .
.
Постоянная времени цепи заряда конденсатора
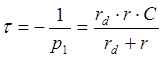 .
.
Подставляя (5) и (6) в (4), получаем формулу напряжения на конденсаторе в процессе его заряда
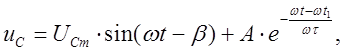 (7)
(7)
где ![]() (7а)
(7а)
![]() - напряжение на
конденсаторе в момент времени
- напряжение на
конденсаторе в момент времени ![]() ;
;
![]() (8)
(8)
Момент времени ![]() определяется
из условия, что ток выпрямителя в этот момент времени равен нулю. Найдём
определяется
из условия, что ток выпрямителя в этот момент времени равен нулю. Найдём ![]() , подставив (7) в (1):
, подставив (7) в (1):
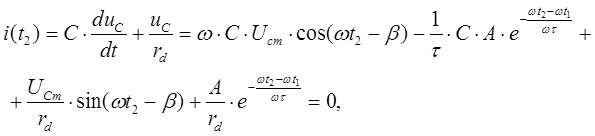
откуда получаем трансцендентное уравнение
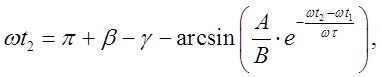 (9)
(9)
где ![]() ;
;
![]() .
.
В момент времени напряжение на конденсаторе достигнет величины
![]() (10)
(10)
вентиль запирается, начинается процесс разряда
конденсатора на сопротивление ![]() (участок II
рис.2).
(участок II
рис.2).
Напряжение на конденсаторе при его разряде изменяется экспоненциально:
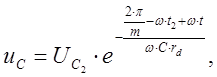 (11)
(11)
где ![]() - параметр выпрямителя,
равный количеству полупериодов тока, пропускаемых вентилями через нагрузку в
течение периода:
- параметр выпрямителя,
равный количеству полупериодов тока, пропускаемых вентилями через нагрузку в
течение периода:
![]() для
схем однополупериодного выпрямления;
для
схем однополупериодного выпрямления;
![]() для
схем двухполупериодного выпрямления.
для
схем двухполупериодного выпрямления.
Разряд конденсатора заканчивается в
момент времени ![]() . Найдём его, приняв (8) и (11)
для
. Найдём его, приняв (8) и (11)
для ![]()
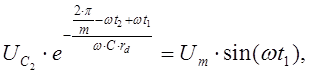
откуда
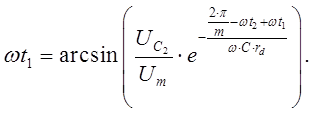 (12)
(12)
Уравнение (12) является трансцендентным и подобно уравнению (9) записано в виде, удобном для решения методом простой итерации /5/.
Среднее значение напряжения пропорционально заряду, протекающему
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.