8. Купола. Конструкция. Основы расчета куполов безмоментной теории
Купольное покр-е сост. из 2 осн-х конструктивн. эл-тов – тонкостенной оболочки и опорного кольца. Если в куполе предусмотрен центральный проем, то устраивают также верхнее кольцо, обрамляющее проем. Купол с непрерывным по контуру шарнирно-подвижным опиранием, совподающим по направл-ю с касат-й к оболочке, явл. статически определимой конструкцией.

 Сборные купола: 1
– панель.
Сборные купола: 1
– панель.
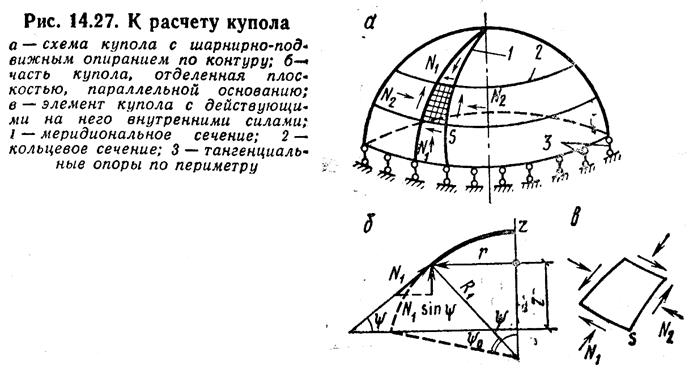
Тонкостенные купола можно рассчитывать по безмоментной теории. Элемент осесимметричного купола, ограниченный двумя меридиональными и двумя кольцевыми сечениями, нах-ся под возд-ем следующих сил: меридиональных N1, кольцевых N2 и касательных S (рис), отнесенных к единице длины сечения. При осесимметричной нагр-ке S = 0. Принимая обозначения ψ – текущая угловая координата; Qψ – нагрузка на сегмент, ограниченный углом ψ, из условия равновесия эл-та купола находят силу N1 и распор H: N1 = Qψ / 2πrsinψ;(1) H = N1 cosψ = (Qψ / 2πr)ctgψ. (2)
Безмоментное напряженное состояние тонкостенных оболочек опис-ся ур-ем равновесия на ось 0Z нагрузки и внутр-х сил, отнесенных к эл-ту единичных размеров основания оболочки. При этом получают N1 / R1 + N2 / R2 = qψ,(3) где qψ – составляющая нагрузки, нормальная к поверхности купола. Если в случае купола с шаровой поверхностью при R1 = R2 = К обозначить нагр-ку от собств. веса купола на единицу пов-ти g, тогда qψ = gcosψ; Qψ = 2πRag.(4) Используя эти ф-лы и зависимости а = R (1 – cosψ); r = R sin ψ, из выражений (1) и (3) находят N1 = Rg / (1 + cosψ); N2 = gRcosψ – Rg / (1 + cosψ). (5) Кольцевое сеч-е, в котором N2 = 0 (шов перехода), определяется углом φ = 51о 49’. Аналогично получают решение для шарового купола при снеговой нагрузке p, которая считается равномерно распредел-й по горизонтальн. проекции и меняющейся по пов-ти купола пропорционально cos ψ: N1 = 0,5 pR; N2 = 0,5 pК cos 2ψ.(6)
Основные нагр-ки, определяющие размеры конструкции купола – собств. вес оболочки вместе с утеплителем и кровлей, а также снеговая нагрузка. Обе нагрузки принимают действующими осесимметрично. Ветровые нагр-ки при пологих купольных покр-ях решающего знач-я не имеют и могут не приниматься во внимание. При высоких куполах, встречающихся реже, усилия от ветровых нагр-к определяют приемами теории упругости.
9. Многоэтажные здания. Рамные, связевые, рамно-связевая схемы. Основы расчетов элементов каркаса
Типы: промышленные, административные, жилые.
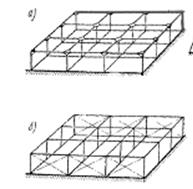
Рамная схема представляет собой систему колонн, ригелей и перекрытий, соединенных в конструктивных узлах в жесткую и устойчивую пространственную систему, воспринимающую горизонтальные (ветровые и другие) усилия.
Связевая схема каркасного здания аналогична рамной схеме с тем лишь дополнением, что горизонтальная жесткость здания увеличивается за счет диагональных связей, выполняемых, как правило, из металла. При этом часть горизонтальных усилий передается с колонн на эти связи. Особенностью рамно-связевой схемы является ограничение перемещений каркаса.
Рамно-связевая схема комбинация двух схем (попериметру зд. Или по высоте одной вертик.пов-ти)
Основными несущими констр-ми многоэтажн. каркасного зд-я явл. ж/б рамы, вертикальные связевые диафрагмы и связующие их междуэтажные перекрытия. При действии горизонтальных нагрузок совместная работа разнотипных верт-ых к-кций в многоэт. зд-ии достиг-ся благодаря высокой жесткости при изгибе в своей плоскости междуэтажн. перекр-й, работающих как горизонтальн. диафрагмы. Важнейш. усл-ем достиж-я высоких эксплуатационных качеств многоэт-го зд-я явл. обеспеч-е его надежн. сопротивл-я горизонтальным нагрузкам и воздействиям.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.