Расчет прогибов ребер. Расчет марша по раскрытию трещин, нормальных к продольной оси

изгибающий момент от действии только постоянных и длительных нагрузок, кН · м;

q_ld – постоянная и длительная нагрузка на марш, кН/м;

l– длина горизонтальной проекции марша, м;

 α – угол наклона марша.

, где q_ld  – постоянная и длительная нагрузка на марш, кН/м;

qⁿ – собственный вес марша, кН/м²;

 –  длительно действующая временная нагрузка, кН/м²;

 а – ширина марша, м;

 γ_f – коэффициент надежности по нагрузке.

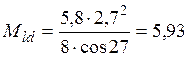 кН/м.

 кН·м.

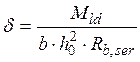, где М_ld –изгибающий момент от действии только постоянных и длительных нагрузок, кН · м.

;

.

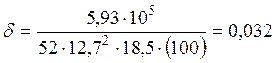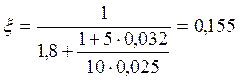Плечо внутренней пары сил при φ_f  = 0

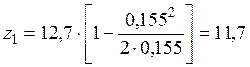 см.

Определяем коэффициент ψ_s по формуле

, где    ψ_s – коэффициент, учитывающий работу растянутого бетона на участке с трещинами;

;

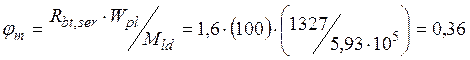φ_ls= 1,1 в соответствии со СНиП 2.03.01-84.

Определяем кривизну 1/r₂ в середине пролета марша от действия только постоянных и длительных нагрузок.

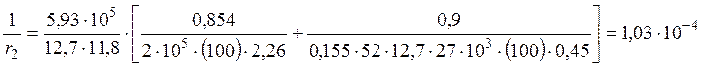 см^-1.

Прогиб f₂  

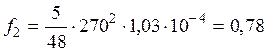 см.

Определение прогиба f₃

Кривизну 1/r₃ при длительном действии постоянной и длительной нагрузок определяем с использованием данных кривизны 1/r₁ и 1/r₂ : М_ld = 5,93  кН·м; ξ = 0,155; z₁ = 11,8 см; φ_m = 0.36. Коэффициент ν = 0,15 при продолжительном действии нагрузки.

Коэффициент ψ_s при φ_ls = 0,8 равен

.

Кривизна 1/r₃ в середине пролета марша

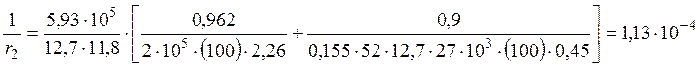 см^-1.

Прогиб f₃  

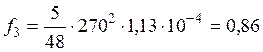 см.

Суммарный прогиб

 см.

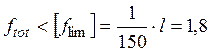 см по конструктивным требованиям и  см – по эстетическим требованиям.

2.4.7 Расчет марша по раскрытию трещин, нормальных к продольной оси

          2.4.7.1 Расчет по длительному раскрытию трещин

Лестничный марш относится к третьей категории трещиностойкости. Предельно допустимая ширина раскрытия трещин составляет а_crc1 = 0,4 мм и а_crc2 = 0,3 мм.

Ширину раскрытия трещин определяем по формуле

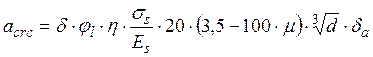, где δ – коэффициент, принимаемый равным 1 для изгибаемых и сжатых элементов;

φ_l – коэффициент, учитывающий вид нагрузок и бетонов, при учете многократно повторяющейся нагрузки, а также длительного действия постоянных и длительных нагрузок  для конструкций из тяжелого бетона естественной влажности ;

 η – коэффициент, зависящий от вида и профиля продольной арматуры, при стержневой арматуре периодического профиля η = 1;

σ_s – напряжения растяжения в стержнях крайнего ряда;

 – коэффициент армирования сечения (без учета сжатых свесов полок), принимаемый не более 0,02;

d– диаметр стержней арматуры, мм;

 δ_а – коэффициент, учитывающий влияние толщины защитного слоя бетона со стороны растянутой арматуры.

; ; δ_а = 1, так как а₂ = 3 см < 0,2 · h = 0,2 · 15,7 = 3,14 см; d = 12 мм.

Ширину длительного раскрытия трещин определяют от длительного действия постоянных и длительных нагрузок.

Определяем напряжение в растянутой зоне

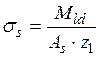, где σ_s - напряжение в растянутой зоне, МПа;

      М_ld –изгибающий момент от действии только постоянных и длительных нагрузок, кН·м;

      А_s – площадь сечения арматуры, см²;

z₁ – плечо внутренней пары сил, см.

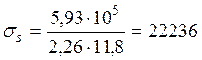 Н/см²  МПа.

Вычисляем ширину раскрытия трещин

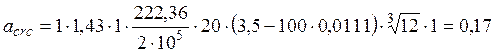 мм <  мм.

Условие выполняется.

2.4.7.2 Расчет по кратковременному раскрытию трещин

Ширину кратковременного раскрытия трещин определяют как сумму ширины раскрытия от длительного действия постоянных и длительных нагрузок a_crc3 и приращения ширины раскрытия от действия кратковременных нагрузок :

, где a_crc – ширина кратковременного раскрытия трещин, мм;

 – приращение ширины раскрытия трещин в результате кратковременного увеличения нагрузки от постоянной и длительной до полной, мм;

a_crc3 – ширина раскрытия трещин от длительного действия постоянных и длительных нагрузок, мм.

a_crc3 = 0,17 мм.

Напряжение в растянутой арматуре при кратковременном действии всех нормативных нагрузок

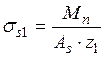, где σ_s1 – напряжение в растянутой арматуре при кратковременном действии всех нормативных нагрузок, МПа;

M_n– момент от полной нормативной нагрузки кН·м;

      А_s – площадь сечения арматуры, см²;

z₁ – плечо внутренней пары сил, см.

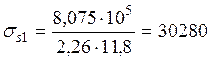 Н/см²  МПа.

Напряжение в растянутой арматуре от действия постоянных и длительных нагрузок

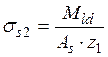, где σ_s2 – напряжение в растянутой арматуре от действия постоянных и длительных нагрузок, МПа;

      М_ld – изгибающий момент от действии только постоянных и длительных нагрузок, кН·м;

      А_s – площадь сечения арматуры, см²;

z₁ – плечо внутренней пары сил, см.

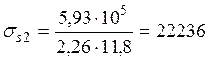 Н/см²  МПа.

Приращение напряжения при кратковременном увеличении нагрузки от длительно действующей до ее полной величины определяем по формуле

, где ∆ σ_s– приращение напряжения при кратковременном увеличении нагрузки от длительно действующей до ее полной величины