Расчет железобетонного лестничного марша шириной 1,05 метра

2.4 Расчет железобетонного лестничного марша

2.4.1  Конструктивное решение лестниц

Расчет произведен для железобетонного лестничного марша шириной

а = 1,05 м, высота этажа 2,8 м, угол наклона марша α = 27°, ступени размером 15,6 × 30 см. Бетон класса В25, арматура каркасов класса А-III, сеток – класса В_Р-I. Расчетное сопротивление арматуры R_s = 355 МПа; расчетная призменная прочность бетона R_b  = 14,5 МПа; расчетное сопротивление при растяжении R_bt = 1,05 МПа; нормативное сопротивление бетона при растяжении R_bt,ser = 1,6 МПа; нормативная призменная прочность  R_b,ser = 18,5 МПа; начальный модуль упругости бетона E_b  = 2,7×10⁴ МПа.

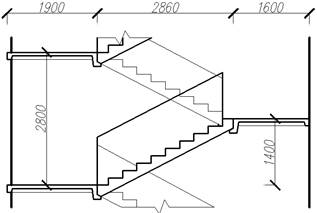
Лестничный марш, расчетная схема, сечение марша приведены на рисунке 1.4.1.

а)                                                             б)

в)                                                                    г)

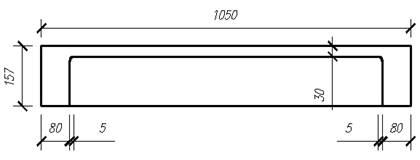
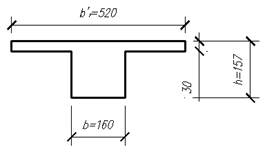
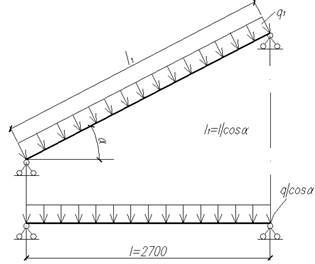
Рисунок 1.4.1 – К расчету лестничного марша:

а – лестничный марш; б – расчетная схема; в – фактическое поперечное сечение; г – приведенное поперечное сечение

2.4.2 Определение нагрузок и усилий

Собственный вес типовых маршей составляет qⁿ = 3,6 кН/м² горизонтальной проекции. Временная нормативная нагрузка для лестниц жилого дома pⁿ = 3 кН/м², коэффициент надежности по нагрузке γ_f = 1,2; длительно действующая временная нагрузка  = l кН/м².

Расчетная нагрузка на марш

, где q – расчетная нагрузка на марш, кН/м;

qⁿ – собственный вес марша, кН/м²;

pⁿ – временная нормативная нагрузка, кН/м²;

а – ширина марша, м;

γ_f – коэффициент надежности по нагрузке.

 кН/м.

Расчетный изгибающий момент в середине пролета марша

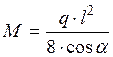, где М – расчетный изгибающий момент в середине пролета марша, кН · м;

q – расчетная нагрузка на 1 м длины марша, кН/м;

l– длина горизонтальной проекции марша, м;

 α – угол наклона марша.

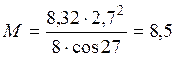 кН·м.

Поперечная сила на опоре

,

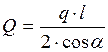где Q – поперечная сила на опоре, кН;

q – расчетная нагрузка на 1 м длины марша, кН/м;

l– длина горизонтальной проекции марша, м;

  α – угол наклона марша.

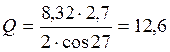кН.

2.4.3 Предварительное назначение размеров сечения марша

Применительно к типовым заводским формам назначаем толщину плиты (по сечению между ступенями)  = 30 мм, высоту ребер (косоуров) h = 157 мм, толщину ребер b_r = 80 мм (рис. 1.4.1, в). Действительное сечение марша заменяем на расчетное тавровое с полкой в сжатой зоне (рис. 1.4.1, г):  мм; ширину полки  при отсутствии поперечных ребер принимаем не более  см или  см, принимаем за расчетное меньшее значение  см.

2.4.4 Подбор площади сечения продольной арматуры

По условию  устанавливаем расчетный случай для таврового сечения (при x = ): при  нейтральная ось проходит в полке.

Здесь М – расчетный изгибающий момент в середине пролета марша, Н·м;

R_b  – расчетная призменная прочность бетона, МПа;

γ_b2 – коэффициент условий работы бетона;

 – ширина полки, см;

 – толщина плиты по сечению между ступенями, см;

h₀ – рабочая высота сечения марша, см.

, где h – высота см;

а – расстояние от центра тяжести растянутой арматуры до внешнего края сечения, см.

 см.

 Н·см, условие удовлетворяется, нейтральная ось проходит в полке; расчет арматуры выполняем по формулам для прямоугольных сечений шириной  = 52 см.

Вычисляем:

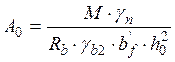, где М – расчетный изгибающий момент в середине пролета марша, кН·м;

R_b  – расчетная призменная прочность бетона, МПа;

 – ширина полки, см;

h₀ – рабочая высота сечения марша, см;

g_n – коэффициент надежности по назначению здания;

γ_b2 – коэффициент условий работы бетона.

;

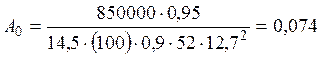по таблице находим η = 0,962; ξ = 0,077;

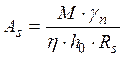, где М – расчетный изгибающий момент в середине пролета марша, кН·м;

R_s – расчетное сопротивление арматуры, МПа;

h₀ – рабочая высота сечения марша, см;

g_n – коэффициент надежности по назначению здания.

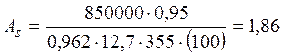 см².

По сортаменту принимаем 2 Æ 12 А-III с площадью A_sp = 2,26 см², что превышает требуемую расчетную площадь на  .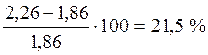

В каждом ребре устанавливаем по одному плоскому каркасу К-1.

2.4.5 Расчет наклонного сечения на поперечную силу

Поперечная сила на опоре

, где Q_max – поперечная сила на опоре от расчетной полной нагрузки, кН;

Q – поперечная сила на опоре от расчетной нагрузки, кН;

g_n – коэффициент надежности по назначению здания.

 кН.

Вычисляем проекцию расчетного наклонного сечения на продольную ось с по формуле.

, где b – толщина расчетного таврового сечения с полкой в сжатой зоне, см;

h₀ – рабочая высота сечения марша, см;

R_bt – расчетное сопротивление бетона при растяжении, МПа;

γ_b2 – коэффициент условий работы бетона;

φ_b2 – коэффициент, принимаемый в зависимости от вида бетона, для тяжелого бетона 2,0.

φ_n = 0; , ; .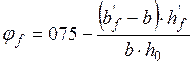

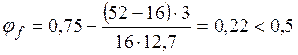 Н/см;

в расчетном наклонном сечении , а так как , то ,  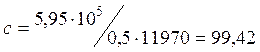см, что больше  см. Тогда ,  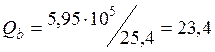 Н  кН, что больше  кН, следовательно, поперечная арматура по расчету не требуется.

В 1/4 пролета назначаем из конструктивных соображений поперечные стержни диаметром 6 мм из стали класса A-I, шагом S = 70 мм (не более