Математическое ожидание случайной величины

Математическим ожиданием СВ называется ее среднее ожидаемое значение:

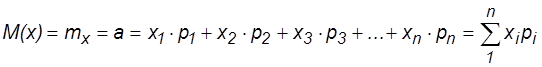, где  х₁, х₂, х₃, ... – возможные значения случайной величины;

р₁, р₂, р₃, ... – вероятности, отвечающие этим возможным значениям;

М(х) – имеет размерность самой случайной величины.

В общем случае М(х) показывает среднее значение СВ, которое можно ожидать при одном испытании из числа многих, проводимых в аналогичных условиях.

Все возможные значения СВ рассеиваются (группируются) около М(х). Поэтому М(х) является центром распределения (рассеивания) СВ, характеристикой места СВ на числовой оси.

Некоторые  характеристики  рассеивания  СВ  около  m_x

Отклонение СВ x от m_x

.

А.  Для  нормального  распределения

Дисперсия СВ (D_x)

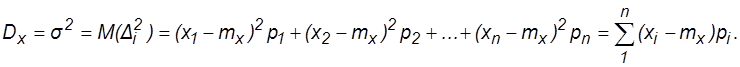
Среднее квадратическое отклонение СВ (s )

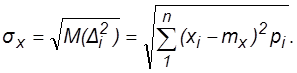
Среднее квадратическое отклонение СВ равно корню квадратному из математического ожидания квадрата отклонения СВ.

Срединное  отклонение  (Е)

Срединным отклонением называется такая величина, относительно которой вероятность получения отклонения по абсолютному значению как меньше, так и больше этой величины, равна половине.

Зависимость между  Е  и s.

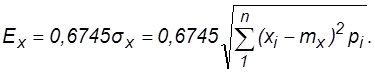
С помощью последней формулы при обосновании правил пристрелки по НЗР определяют срединную ошибку пристрелки Rд.