Равновесное состояние и концентрации подвижных зарядов в полупроводниках

Пионеры и их детище

В 1947г. физики В.Шокли (сидит), Дж. Бардин (слева), У. Браттейн разработали точечный транзистор—первый полупроводниковый прибор (см. рис. справа). В 1956 все трое получили Нобелевскую премию по физике. (Бардин — единственный в мире физик—дважды Нобель – еще и в 1972  г.)

Другие первые полупроводниковые приборы и интегральные схемы приведены на рисунках ниже.

Ключевые вопросы

– почему планарный транзистор на левом рисунке имел форму капли?

– кто и когда сделал самую первую интегральную схему?

Ключевая задача темы «Равновесное состояние и концентрации подвижных зарядов в полупроводниках»

Предположим, что в некотором полупроводнике собственная концентрация равна 8 мкм^-3. Не меняя температуры полупроводника, его залегировали донорной примесью с концентрацией 12 мкм^-3, которая полностью ионизовалась, а затем  полупроводник перешел в состояние термодинамического (теплового) равновесия. Спрашивается – чему в данном случае равна концентрация основных и неосновных носителей заряда?

Студент решил задачу следующим образом. В начальный момент (без легирования) n=p=n_i=8. После введения донорной примеси, которая полностью ионизовалась, в зоне проводимости добавилось 12 электронов/мкм³, а в валентной зоне остались те же 8 дырок/мкм³. Таким образом, в примесном полупроводнике концентрация основных носителей составит 8+12=20электронов/мкм³, а неосновных – 8 дырок/мкм³.

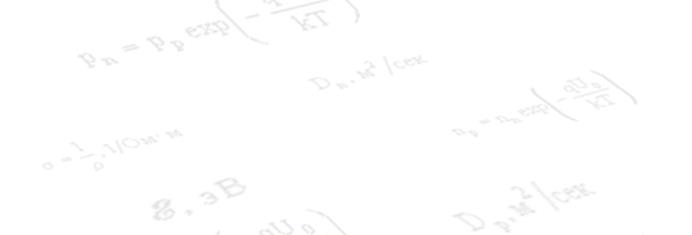Преподаватель предложил студенту записать основные теоретические соотношения для нахождения концентраций носителей в полупроводниках в состоянии равновесия и проверить их на данном числовом примере. Студент быстро ответил: «Первое фундаментальное уравнение – это уравнение электронейтральности. Т.е. сумма всех положительных зарядов должна равняться сумме всех отрицательных зарядов в любой произвольно выбранной точке полупроводника. Из отрицательных зарядов у нас есть только подвижный заряд электронов. Их ровно 20 шт. на 1 мкм³. Считаем положительный заряд. Он состоит из подвижного заряда дырок. Их 8 шт. И неподвижного заряда ионизированных доноров. По условию их 12шт. Очевидно, что уравнение электронейтральности выполняется. Вторым фундаментальным уравнением является уравнение закона сохранения масс. Т.е. в состоянии равновесия в любой момент времени произведение концентраций основных и неосновных носителей должно быть равно квадрату собственной концентрации. Произведение подвижных носителей у нас 20*8=160, а квадрат собственной концентрации равен 8*8=64. Но 64 не равно 160! Что-то здесь не так…». Студент задумался.

В чем же дело и правильно ли была решена исходная задача?

Ключевая задача  

темы «Электростатические поля в полупроводниках»

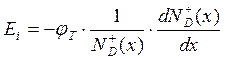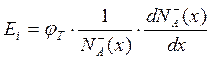Студент на экзамене отвечает на вопрос – “Встроенное поле в полупроводниках”. Подробно объяснив физические механизмы, лежащие в основе явления, студент выписывает формулы для напряженности поля:  для полупроводника n-типа и  для полупроводника p-типа, где  и - концентрационные профили легирования. Посмотрев на выписанные формулы, преподаватель анализирует их с помощью уточняющих вопросов к студенту: “Если концентрация легирующей примеси будет монотонно убывать, например, линейно, и при этом стремиться к нулю, тогда получается, что поле будет стремительно увеличиваться к бесконечности и в собственном полупроводнике должны возникать поля, приводящие к его разрушению вследствие электрического пробоя. Так ли это?” Студент задумался. Помогите ему ответить на заданный вопрос.

Ключевая задача 

темы «Компоненты тока в полупроводниках»

Студент на экзамене отвечает на вопрос – «Диффузионная компонента электрического тока в полупроводниках». Подробно раскрыв физическую сущность данного явления, студент выписывает формулы для электронной и дырочной компонент плотностей тока: 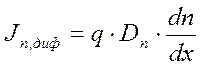; 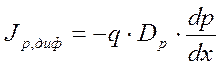и по своей инициативе в завершении ответа разъясняет преподавателю, что знак минус в формуле для  связан с тем, что у дырок заряд – положительный и диффузионный поток по закону Фика всегда направлен в противоположную к градиенту сторону (плюс умножить на минус есть минус), а для  - знак положительный, т.к. заряд у электронов – отрицательный (минус на минус есть плюс). Преподаватель, согласившись с данным утверждением студента, резонно замечает, что примерно такая же асимметрия в знаках должна выполняться и для формул у дрейфовой компоненты тока - ; . Почему же там она не наблюдается? Студент задумался. В чем же здесь дело?

Ключевая задача темы «Собственная и примесная электропроводность в полупроводниках»

(неужели открытие?)

Тщательно изучив темы «собственные и примесные полупроводники» и «компоненты тока в полупроводниках» Студент замечает, что можно предложить совершенно новое теоретическое определение типа полупроводника: в экспериментальном образце измеряем электронную и дрейфовую компоненты тока; если компоненты равны — полупроводник собственного типа, если электронный ток больше дырочного — то полупроводник электронный, если наоборот — то дырочный. Ни в одном из рекомендованных лектором учебников нет такой классификационной схемы!! Неужели Студент стоит на пороге открытия?

Помогите ему разобраться в его рассуждениях.

Ключевая задача 

темы «Процессы генерации-рекомбинации носителей заряда неравновесного полупроводника»

Студент на экзамене отвечает на вопрос о релаксации фотовозбужденных неосновных носителей в полупроводнике n-типа. Он записывает уравнение непрерывности с учетом однородности распределения концентраций неосновных носителей и потенциала в объеме полупроводника после выключения засветки, а так же общее решение получающегося простейшего однородного дифференциального уравнения первого порядка. Студент разъясняет преподавателю, что константа С, входящая в общее решение находится из начальных условий: в момент выключения засветки t=0 концентрация неравновесных носителей равняется G₀×t_p. В заключение ответа он поясняет, что при этом происходит переход от стационарного состояния полупроводника к равновесному. Преподаватель, согласившись с рассуждениями студента спрашивает — «А как изменится уравнение непрерывности, начальное условие и решение уравнения, если все происходит с точностью до наоборот — в начале полупроводник находится в равновесном состоянии, а в момент t=0 включают засветку?» Студент задумался. Помогите ему найти решение задачи.

Ключевая задача 1

для темы “Модели резисторов”

 

Рисунок-Пленочный резистор трапециидальной формы

Предположим, что форма тонкопленочного резистора (вид сверху) не прямоугольная, а трапециидальная. Чему будет равно в этом случае сопротивление резистора толщиной H? ( Удельное сопротивление r). Ответ: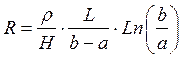

Ключевая задача №2

для темы “Модели резисторов”

Как, зная коэффициент формы и R_S для резистора

 

, вычислить сопротивление резистора                          ?

Ключевая задача №3

для темы “Модели резисторов”

Вычислить коэффициент формы для резистора с внутренним контактом