Построение многоаргументных квазилинейных моделей

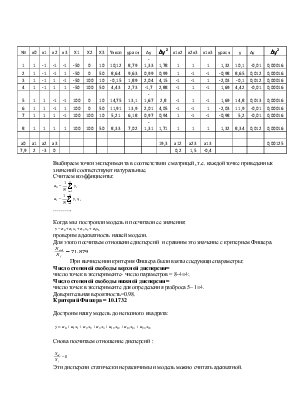
Отчет по лабораторной работе №2.

Построение многоаргументных квазилинейных моделей.

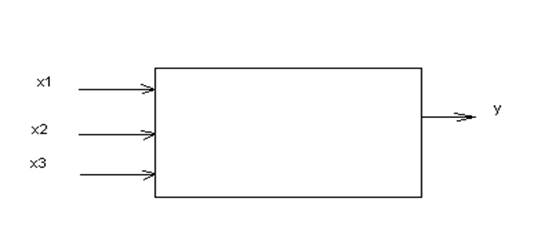
Линейная модель имеет вид:

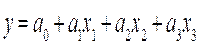
Для построения многоаргументной квазилинейной модели используется метод наименьших квадратов:

Выбирается N – число точек, количество аргументов n дано в  эксперименте.

Каждой точке записываем отклонение:

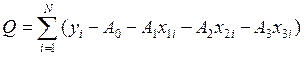
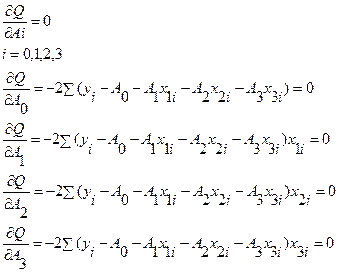
Расписываем что в скобках по суммам:

…….

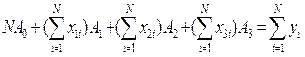
СЛАУ относительно A_{i .}

_{1)Условие симметрии относительно центра:}

2)Условие ортогональности

3)Условие нормировки

Отсюда получается:

…

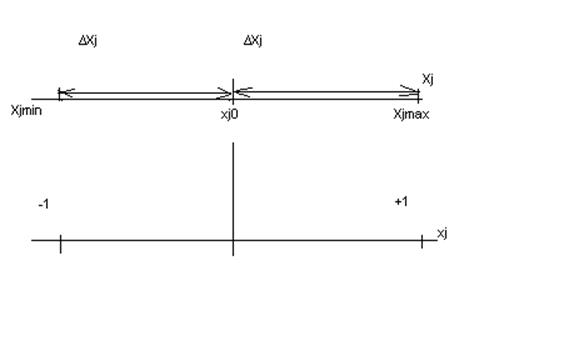
Для того чтобы выполнить эти условия выполняем преобразование переменных от Хбол к Xмал.

Теперь условия будут выполняться для нормированных значений:

Расчеты для определения параметров модели и проверки адекватности представлены в след.таблице:

Выбираем точки эксперимента в соответствии с матрицей, т.е. каждой точке приведенных значений соответствуют натуральные.

Считаем коэффициенты:

……….

Когда мы  построили модель и посчитали ее значения:

проверим адекватность нашей модели.

Для этого посчитаем отношение дисперсий  и сравним это значение с критерием Фишера.

При вычислении критерия Фишера были взяты следующие параметры:

Число степеней свободы верхней дисперсии=

число точек в эксперименте- число параметров = 8-4=4;

Число степеней свободы нижней дисперсии=

число точек в эксперименте для определения разброса 5– 1=4.

Доверительная вероятность=0.98.

         Критерий Фишера = 10.1732

Достроим нашу модель до неполного квадрата:

Снова посчитаем отношение дисперсий :

Эти дисперсии статически неразличимы и модель можно считать адекватной.