Синтез последовательностных автоматов. Проектирование автомата Муру и Мили на RS- D-триггерах в базисе ИЛИ-НЕ

Министерство образования и науки Российской Федерации

НГТУ

Курсовая работа

Микросхематехника

Синтез последовательностных автоматов студент:     Егоркин А. В.

группа:      РМ2–71

проверил: Хабаров С. П.

дата:

Новосибирск 2009

Цель работы.

Спроектировать автомат Муру и Мили на RS- D-триггерах в базисе ИЛИ – НЕ, который генерирует заданные последовательности.

Заданные последовательности:

0 – 8 – 2 – 1 – 5 – 9 –12

0 – 9 – 1 – 15 – 2 – 11 –7 –4

Общие теоретические сведения.

Структура автомата последовательностного типа:

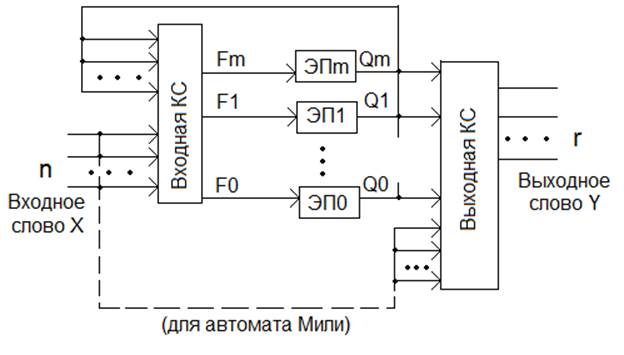
– здесь F_i и Q_i – входные информационные сигналы и переменная состояния    i-ого элемента памяти соответственно. Если в качестве элементов памяти используются парафазные триггеры, то у каждого элемента памяти одновременно присутствуют два состояния переменной Qi – прямое и инверсное. Для элементов памяти на двухвходовых триггерах каждый информационный пакет F_i состоит из двух переменных – S_i (или J_i) и R_i (или K_i).

Различают автоматы Мили и Мура. В автомате Мура выходное слово Y формируется только на основе информации в элементах памяти Q. В автомате Мили выходное слово Y получается как на элементов памяти Q, так и на основе входного слова X (где X, Q, Y – векторы).

Автомат Мура: 

Автомат Мили:

X_i – входное слово, где i=1,2,…,N.

Y_j – выходное слово (совокупность разрядов), где j=1,2,…,S.

В проектируемом автомате для каждого входного слова X_i на выходе генерируется последовательность различных кодов Y_k, k=1,…,k_Ci.

K_Ci – коэффициент счёта i-ой последовательности (т.е. соответствующей входному слову X_i).

m – количество триггеров, необходимое для генерирования всех последовательностей. Оно определяется максимальным коэффициентом счёта max{ k_ci }.

Количество входов автомата n связано с числом входных слов N условием

.

Количество выходов автомата (выходной комбинационной схемы) равно:

, где R=max{Y_i}.

Триггеры – элементарные автоматы, содержащие собственно элемент памяти (фиксатор) и схему управления.

В данном проектировании будут использоваться RS- и D-триггеры.

Логическая схема бистабильной ячейки (фиксатора):

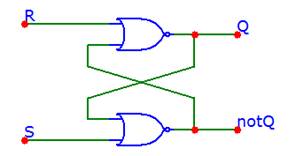
– где  S – set

R – reset

Логическая схема синхронного RS-триггера:

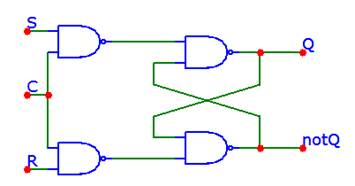
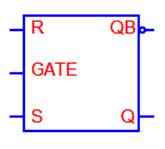
С – синхровход. При С=0 триггер хранит информацию и нечувствителен к изменению потенциала.

Схема D-триггера:

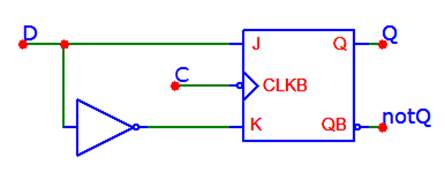
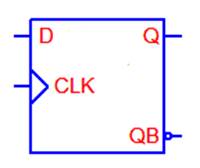
Таблицы истинности используемых триггеров.

RS-триггер					D-триггер
R	S	Qt	Qt+1		D	Qt	Qt+1
0	0	0	0		0	0	0
0	0	1	1
0	1	0	1		0	1	0
0	1	1	1
1	0	0	0		1	0	1
1	0	1	0
1	1	0	x		1	1	1
1	1	1	x

Обратная таблица переходов используемых триггеров.

Проектирование последовательностных автоматов.

В данной работе проектируется генератор числовых последовательностей. Для поиска наиболее оптимального варианта будут найдены и записаны входные функции автоматов Мура и Мили на RS- и D-триггерах. Далее, из 4-х вариантов будет выбран оптимальный, который и будет давать, в результате синтеза полученных функций с использованием компьютерной программы, логическую схему автомата.

На вход автомата будет подаваться единственное входное слово Х, равное «0», если нужно сгенерировать 1-ую последовательность, или «1» – для 2-ой последовательности.

Автомат Мили на RS-триггерах.

Таблица истинности.

Nc	X	Q2	Q1	Q0	Q2	Q1	Q0	RS2		RS1		RS0		Y3	Y2	Y1	Y0
		t			t+1			R2	S2	R1	S1	R0	S0
0	0	0	0	0	0	0	1	x	0	x	0	0	1	0	0	0	0
8	0	0	0	1	0	1	0	x	0	0	1	1	0	1	0	0	0
2	0	0	1	0	0	1	1	x	0	0	x	0	1	0	0	1	0
1	0	0	1	1	1	0	0	0	1	1	0	1	0	0	0	0	1
5	0	1	0	0	1	0	1	0	x	x	0	0	1	0	1	0	1
9	0	1	0	1	1	1	0	0	x	0	1	1	0	1	0	0	1
12	0	1	1	0	0	0	0	1	0	1	0	x	0	1	1	0	0
x	0	1	1	1	x	x	x	x	x	x	x	x	x	x	x	x	x
0	1	0	0	0	0	0	1	x	0	x	0	0	1	0	0	0	0
9	1	0	0	1	0	1	0	x	0	0	1	1	0	1	0	0	1
1	1	0	1	0	0	1	1	x	0	0	x	0	1	0	0	0	1
15	1	0	1	1	1	0	0	0	1	1	0	1	0	1	1	1	1
2	1	1	0	0	1	0	1	0	x	x	0	0	1	0	0	1	0
11	1	1	0	1	1	1	0	0	x	0	1	1	0	1	0	1	1
7	1	1	1	0	1	1	1	0	x	0	x	0	1	0	1	1	1
4	1	1	1	1	0	0	0	1	0	1	0	1	0	0	1	0	0