Определение корней (вещественных и комплексных) уравнения методом Ньютона

Министерство Образования и Науки Российской Федерации

НГТУ

Кафедра Полупроводниковых Приборов и Микроэлектроники

РГЗ по информатике 3-семестр

Факультет: РЭФ

Группа: РМС7-71

Сделал: Кохно Константин Сергеевич

Проверил: Лобач Олег Викторович

Новосибирск 2008

Задание №19

Методом Ньютона найти корни (вещественные и комплексные) уравнения:

при     a₀ = -10.0, a₁ = 18.0,  a₂ = -10.0, a₃ = 2.0, a₄ = -1.0, a₅ = 0.4.

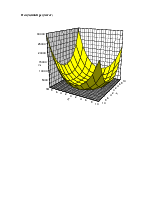
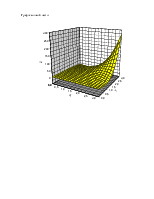
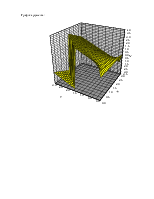
Построить график модуля левой части уравнения в пределах изменения вещественной и мнимых частей z от -10 до +10.

Решение нелинейного уравнения с комплексными корнями

левая часть уравнения

                                                                                                       (1)

представляет собой комплексную величину,  у которой в точке корня должна обратиться в нуль действительная и мнимая части:

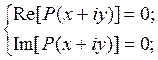                                                                           (2)

Поэтому исходное уравнение превращается в систему двух вещественных уравнений относительно вещественных неизвестных x и y, но при вычислении левых частей уравнений используются комплексные величины. Эта система может быть решена методом Ньютона с помощью функции RootSysNewton().

Решение уравнения:

При решении уравнения используется функция RootSysNewton из модуля ROOT.cpp

Код управляющей программы:

//  управляющая программа для нахождения комплексных корней

//  с помощью RootSysNewton

#include <iostream.h>

#include <stdio.h>

#include <conio.h>

#include "root.h"

int Systema(Vector X, Vector Fx);  // прототип функции - системы уравнений

void main()

{

// описание данных

int i,n,limit,KeyDemo,Nckl,Err;

double epsX,epsF,IDXI,IFxI;

Vector X,Fx;

// задание входных данных

n=2;                  // число уравнений

X[1]=1  ;         // нулевые приближения корней

X[2]=1  ;

epsX=1E-07;        // погрешность вычисления корней

epsF=1E-07;        // погрешность невязки левой части с нулем

// обращение к RootSysNewton

clrscr();

Err=RootSysNewton(Systema,n,epsX,epsF, X,Fx,IDXI,IFxI,Nckl);

// вывод выходных данных

cout<<endl;

cout<<"  Err = "<<Err<<endl;

cout<<" Nckl = "<<Nckl<<endl;

cout<<endl;

for (i=1; i<=n; i++)

printf("X[%1d] = %10.8f   Fx[%1d] = %12.5E\n",i,X[i],i,Fx[i]);

cout<<endl;

printf("IDXI = %12.5E\n",IDXI);

printf("IFxI = %12.5E\n",IFxI);

getch();

}

#include <complex.h>

int Systema(Vector X, Vector F)

{

// описание данных

int i,n;

Vector A;

complex z,Sum;

// задание полинома

n=5;

A[0]=-10.0;

A[1]= 18.0;

A[2]=-10.0;

A[3]= 2.0;

A[4]=-1.0;

A[5]= 0.4;

// формирование левых частей уравнений

z= complex(X[1],X[2]);

Sum=complex(0,0);

for (i=0; i<=n; i++)

Sum+=A[i]*pow(z,i);

F[1]=real(Sum);

F[2]=imag(Sum);

return 0; }

Полученные результаты:

Err = 0

Nckl = 7

X[1] = 1.16196332   Fx[1] =  1.38778E-15

X[2] = 0.29225405   Fx[2] = -8.88178E-16

IDXI =  8.97721E-13

IFxI =  1.64766E-15

Построение графика:

Для построения графика модуля левой части уравнения воспользуемся функцией abs(complex) заголовок которой имеется в файле <complex.h> - стандартные библиотеки.

Также воспользуемся функцией WriteSurfFunc из модуля  “datafile.h”

Код программы:

// Программа для расчета графика функции

#include "datafile.h"

double Fxy(double,double); // прототип отстраиваемой функции

void main()

{

// описание данных

int NpntX,NpntY,keyDemo;

double Xmin,Xmax,Ymin,Ymax;

// ввод входных данных

Xmin=-10; Xmax= 10; NpntX=20;

Ymin=-10; Ymax= 10; NpntY=20;

keyDemo=2;

// расчет и вывод выходных данных в файл

WriteSurfFunc(Fxy,Xmin,Xmax,NpntX,

Ymin,Ymax,NpntY,

keyDemo);

}

#include <complex.h>

double Fxy(double x, double y)

{

complex Z;

double  Fz,a,b,c,d,e,f;

a=-10.0;

b= 18.0;

c=-10.0;

d=  2.0;

e=- 1.0;

f=  0.4;

Z=complex(x,y);

Fz=abs(

a+

b*Z+

c*pow(Z,complex(2,0))+

d*pow(Z,complex(3,0))+

e*pow(Z,complex(4,0))+

f*pow(Z,complex(4,0))

);

return Fz;

}

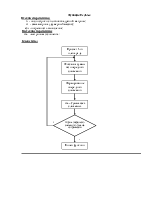
Описание устройства программы:

Как работать с функцией WriteSurfFunc из модуля  “datafile.h” подтобно описано в вышеупомянутом модуле.

Интерес представляет то, как устроена функция double Fxy(double x,double y):

Список входных и выходных параметров видно из этого описания.