Определение корней (вещественных и комплексных) уравнения методом Ньютона, страница 2

Внутри самой функции есть строки:

Fz=abs(

a+

b*Z+

c*pow(Z,complex(2,0))+

d*pow(Z,complex(3,0))+

e*pow(Z,complex(4,0))+

f*pow(Z,complex(4,0))

);

Где f,b,c,d,e,f, -  это коэффициенты нашей функции(полинома).

Функция pow(complex a, complex b) описана в заголовочном файле <complex.h> и возводит комплексную переменную в указанную степень.

Функция abs(complex) описана в том же модуле и именно она и возвращает модуль нашей функции.

Полученный результат:

 

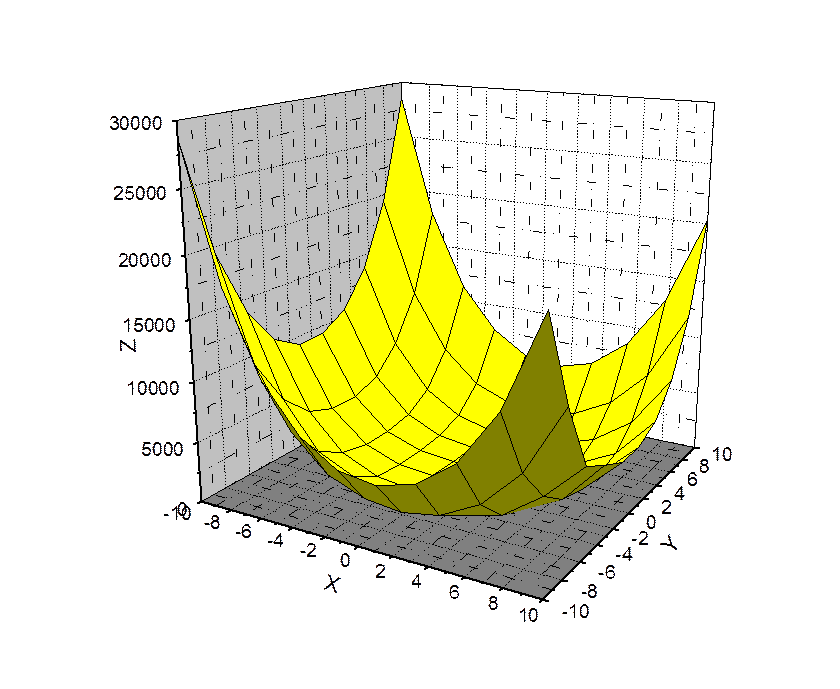
Код упраляющей программы:

#include "define.h"

#include "matrix.h"

#include <conio.h>

#include <iostream.h>

void main()

{

// описание переменных

Matrix A;   // матрица

Matrix Ae;   // результат

int n;      // размерность матрицы

double eps; // погрешность

// ввод матрицы

clrscr();

n=3;

A[1][1]=1; A[1][2]=0; A[1][3]=1;

A[2][1]=0; A[2][2]=1; A[2][3]=0;

A[3][1]=2; A[3][2]=0; A[3][3]=2;

eps=10E-8;

//         InpMat(n,n,A);

//         clrscr(); cout<<"погрешность вычисления: "; cin>>eps;

// расчет матричнй экспоненты

clrscr();

ExpMat(n,A,Ae,eps);

// вывод результата

cout<<endl<<"Полученная матрица:"<<endl<<endl;

OutMat(n,n,Ae,5,5);

getch();

}

Пример работы программы:

Расчет матричной экспоненты:

Исходная матрица:

1   0   1

0   1   0

2   0   2

m(количество слагаемых) = 7

eps = 1e-07

Полученная матрица:

5.68778      0  4.68778

0  2.69103      0

9.37556      0  10.37556

Функция ExpMat:

Входные переменные:                                              

n   - число строк и столбцов квадратной матрицы;             

A   - сама матрица (двумерный массив);                       

eps - погрешность вычисления; 

Выходные переменные

Ae   - матричная экспонента;                                   

 Блок схема:

 

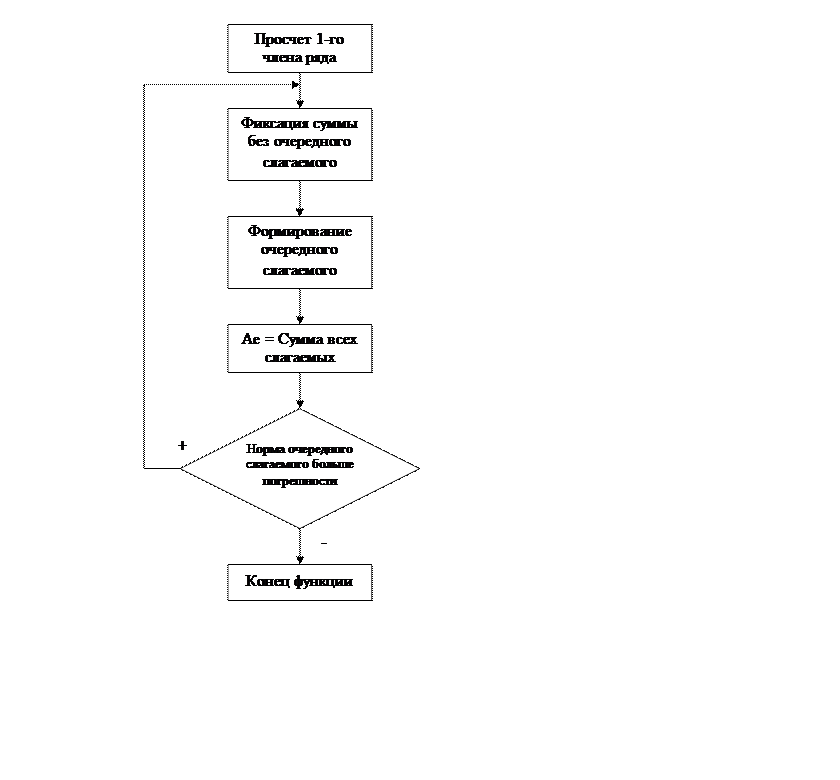
Код программы:

// Программа для расчета графика функции

#include "datafile.h"

#include <math.h>

double Fxy(double,double); // прототип отстраиваемой функции

void main()

{

// описание данных

int NpntX,NpntY,keyDemo;

double Xmin,Xmax,Ymin,Ymax;

// ввод входных данных

Xmin=  0; Xmax= M_PI; NpntX=20;

Ymin=  0; Ymax= M_PI; NpntY=20;

keyDemo=0;

// расчет и вывод выходных данных в файл

WriteSurfFunc(Fxy,Xmin,Xmax,NpntX,

Ymin,Ymax,NpntY,

keyDemo);

}

#include <complex.h>

double Fxy(double x, double y)

{

complex Z;

Z=exp(complex(x,y))*sin(complex(x,y));

return real(Z);

}

Примечание:

Чтобы построить различные графики будем менять вместо real в  последней строке на imag, abs и arg.

Полученные результаты:

График вещественной части:

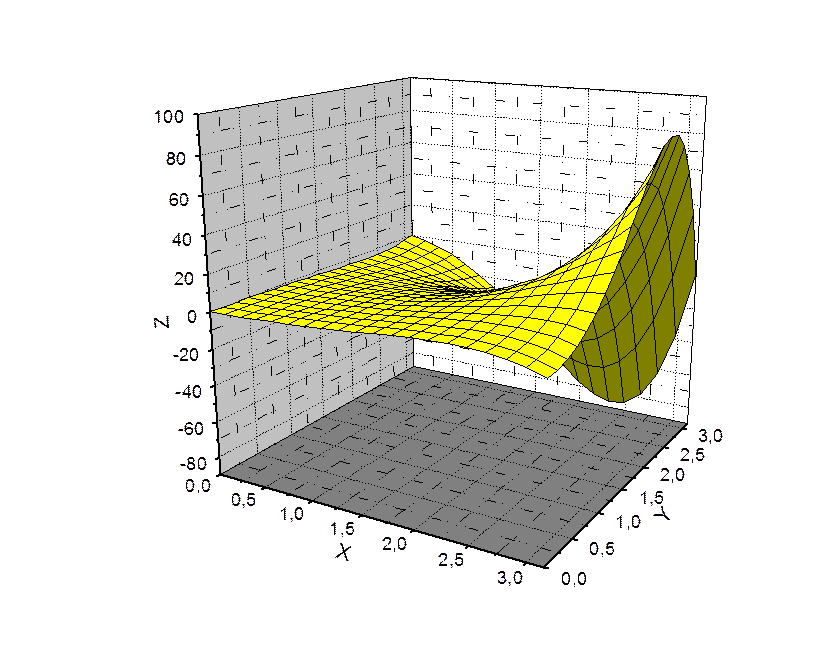
График мнимой части:

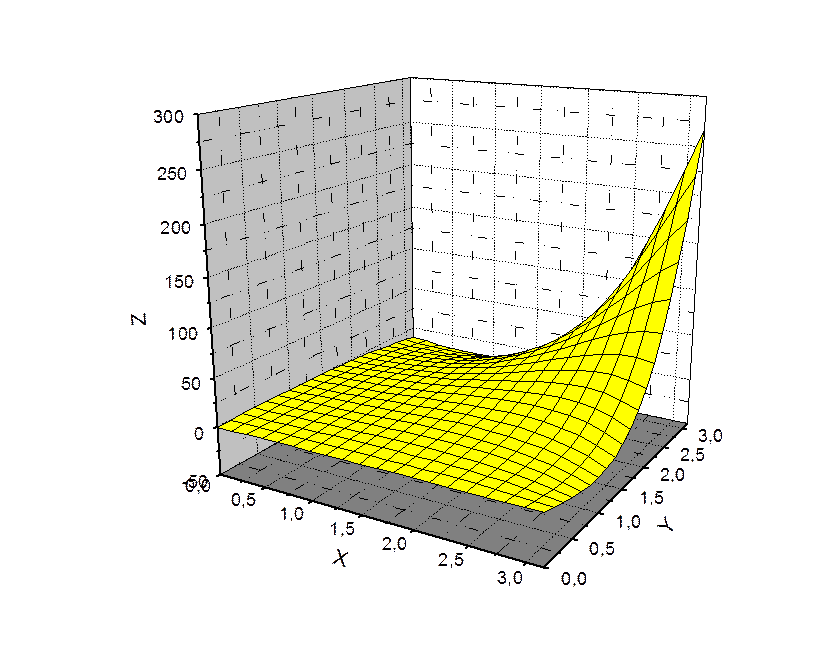
График аргумента:

График модуля:

 Построение следующих 2-х графиков:

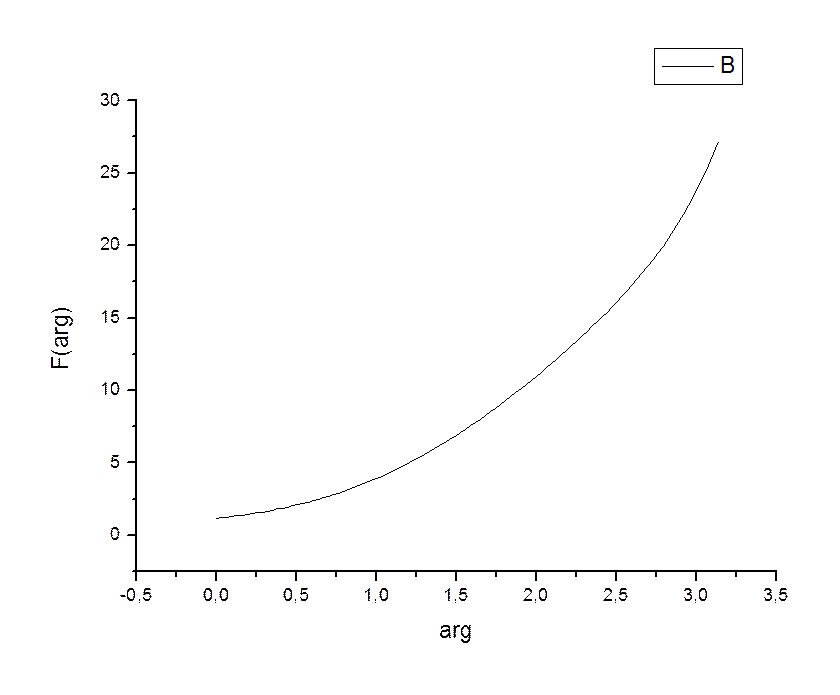
Представить модуль этой функции в виде двух семейств зависимостей (1 - от вещественной части аргумента при параметре мнимой и 2 - от мнимой при параметре – вещественной).

1)параметр мнимой части зададим равным 1.

Код функции изменится:

// Программа для расчета графика функции

#include "datafile.h"

#include <math.h>

double Fx(double); // прототип отстраиваемой функции

void main()

{

// описание данных

int NpntX,keyDemo;

double Xmin,Xmax;;

// ввод входных данных

Xmin=  0; Xmax= M_PI; NpntX=100;

keyDemo=0;

// расчет и вывод выходных данных в файл

WriteFunc(Fx,Xmin,Xmax,NpntX,keyDemo);

}

#include <complex.h>

double Fx(double x)

{

double y=1;

complex Z;

Z=exp(complex(x,y))*sin(complex(x,y));

return abs(Z);

}

Полученный график:

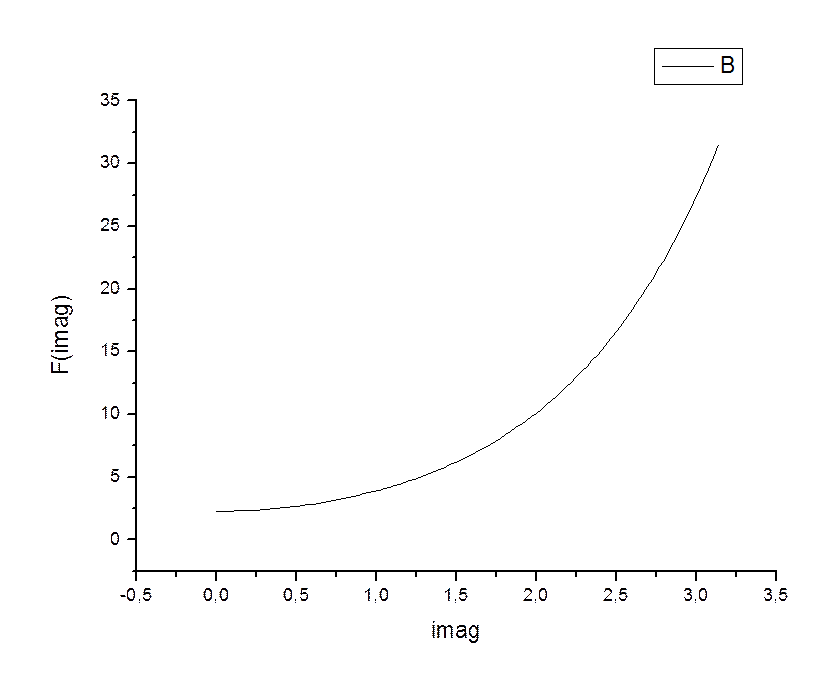
2)параметр вещественной части зададим равным 1.

В программе поменяем местами х и у

Код управляющей программы:

// Программа для расчета графика функции

#include "datafile.h"

#include <math.h>

double Fx(double); // прототип отстраиваемой функции

void main()

{

// описание данных

int NpntX,keyDemo;

double Xmin,Xmax;;

// ввод входных данных

Xmin=  0; Xmax= M_PI; NpntX=100;

keyDemo=0;

// расчет и вывод выходных данных в файл

WriteFunc(Fx,Xmin,Xmax,NpntX,keyDemo);

}

#include <complex.h>

double Fx(double y)

{

double x=1;

complex Z;

Z=exp(complex(x,y))*sin(complex(x,y));

return abs(Z);

}

Полученный график:

Вывод:

Два последних графика на плоскости доказывают истинность построенной поверхности для модуля.