НГТУ, факультет РЭФ, кафедра ППиМЭ |
Лабораторный практикум «Информатика-3»Алгоритмы и программы вычислительных задачмикро- и наноэлектроники |
Лабораторная работа № 2 |
Решение нелинейных алгебраических уравнений и их систем |
© Н.В.Усольцев Редакция 2008 г. Вариант № 1 от 20.09.08 |
В научно-технических расчетах часто встречаются нелинейные уравнения вида
![]() , (1)
, (1)
где
F(x) - некоторая нелинейная (трансцендентная) функция. Вид ее не позволяет
выразить x и найти корень аналитическими методами. Численные же методы
позволяют найти приближенное значение корня уравнения с заданной точностью.
Некоторые из них требуют задания интервала, на котором предполагается корень (A, B), другие - начального (нулевого)
приближения корня ![]() . Значение корня ищется путем
последовательных приближений (итераций), которые циклически совершаются по
определенному итерационному алгоритму.
. Значение корня ищется путем
последовательных приближений (итераций), которые циклически совершаются по
определенному итерационному алгоритму.
![]()
Число итераций заранее определить нельзя – они совершаются до выполнения некоторых условий. Например:
![]() (2a)
(2a)
![]() (2b)
(2b)
где
![]() - заданная абсолютная погрешность
определения корня;
- заданная абсолютная погрешность
определения корня;
![]() - заданная погрешность невязки левой части
уравнения с нулем.
- заданная погрешность невязки левой части
уравнения с нулем.
В лабораторной работе изучаются методы простых итераций, половинного деления (бисекции) и Ньютона.
Система из n нелинейных уравнений относительно n неизвестных может быть представлена в развернутом виде:
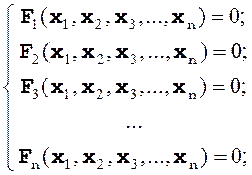 (3)
(3)
или в более компактном – векторном:
![]() , (4)
, (4)
где
![]() - вектор левых частей уравнений, а
- вектор левых частей уравнений, а ![]() - вектор неизвестных, который необходимо
найти. В левые части уравнений может входить любое число параметров.
- вектор неизвестных, который необходимо
найти. В левые части уравнений может входить любое число параметров.
Для решения систем уравнений также используются итерационные методы: Якоби и Зейделя (аналоги метода простых итераций), а также метод Ньютона. В данной работе изучается только метод Ньютона.
Итерационный
процесс решения системы уравнений может быть представлен аналогичной схемой, в
которой неизвестная величина представляет собой вектор ![]()
![]()
Итерации выполняются до тех пор, пока не будут выполнены условия малости модулей векторов
![]() (5а)
(5а)
![]() (5б)
(5б)
Необходимо представлять, что итерации могут сходиться к искомому решению, расходиться от него, а также зацикливаться при неправильном задании погрешностей.
Применение этого метода требует предварительного приведения уравнения к виду
![]() (6)
(6)
Это
легко сделать прибавлением ![]() к левой и правой частям
уравнения в первоначальном виде:
к левой и правой частям
уравнения в первоначальном виде:
![]() .
.
Из (6) легко получается итерационная формула:
![]() (7)
(7)
Итерации выполняются по ней до тех пор, пока не будет выполняться условие (2a). Условие (2b) в этом методе не может быть использовано.
Итерационный процесс сходится к значению корня, если на интервале итераций выполняется условие:
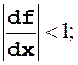 (8)
(8)
Графическая
интерпретация метод простых итераций представлена на рис. 1. В одной системе
координат изображена зависимость левой (![]() ) и
правой (
) и
правой (![]() ) частей формулы (6). Координата
) частей формулы (6). Координата ![]() точки 9 пересечения линий есть искомое
значение корня. Пусть на (k-1)-ой итерации было получено
значение
точки 9 пересечения линий есть искомое
значение корня. Пусть на (k-1)-ой итерации было получено
значение ![]() . Вычислив значение правой части от этого
аргумента (точка 2), сносим это значение на график левой части (точка 3).
Координата
. Вычислив значение правой части от этого
аргумента (точка 2), сносим это значение на график левой части (точка 3).
Координата ![]() точки 3 (точка 4) дает новое значение
неизвестной
точки 3 (точка 4) дает новое значение
неизвестной ![]() . Повторяя итерационные действия (точки
4-5-6-7), получаем следующее приближение
. Повторяя итерационные действия (точки
4-5-6-7), получаем следующее приближение ![]() . Видно,
что этот процесс движется к искомому значению корня.
. Видно,
что этот процесс движется к искомому значению корня.
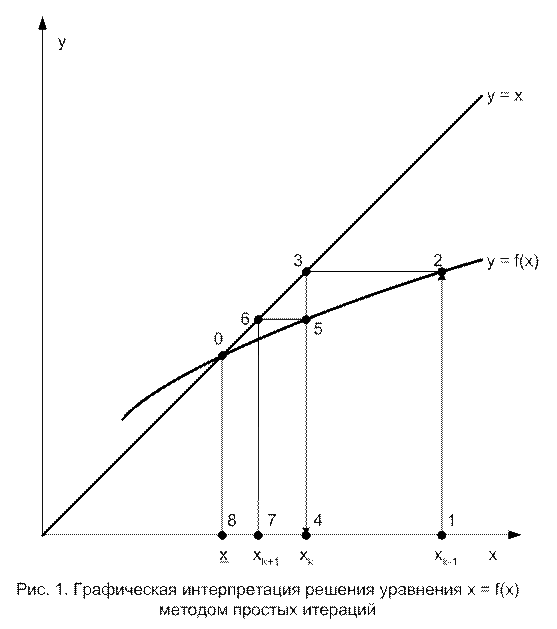
Если график правой части имеет угловой коэффициент, больший единицы (условие 8 не выполняется), то описаные выше итерационные действия приводят к движению от корня. Предлагаем нарисовать и убедиться в этом самостоятельно.
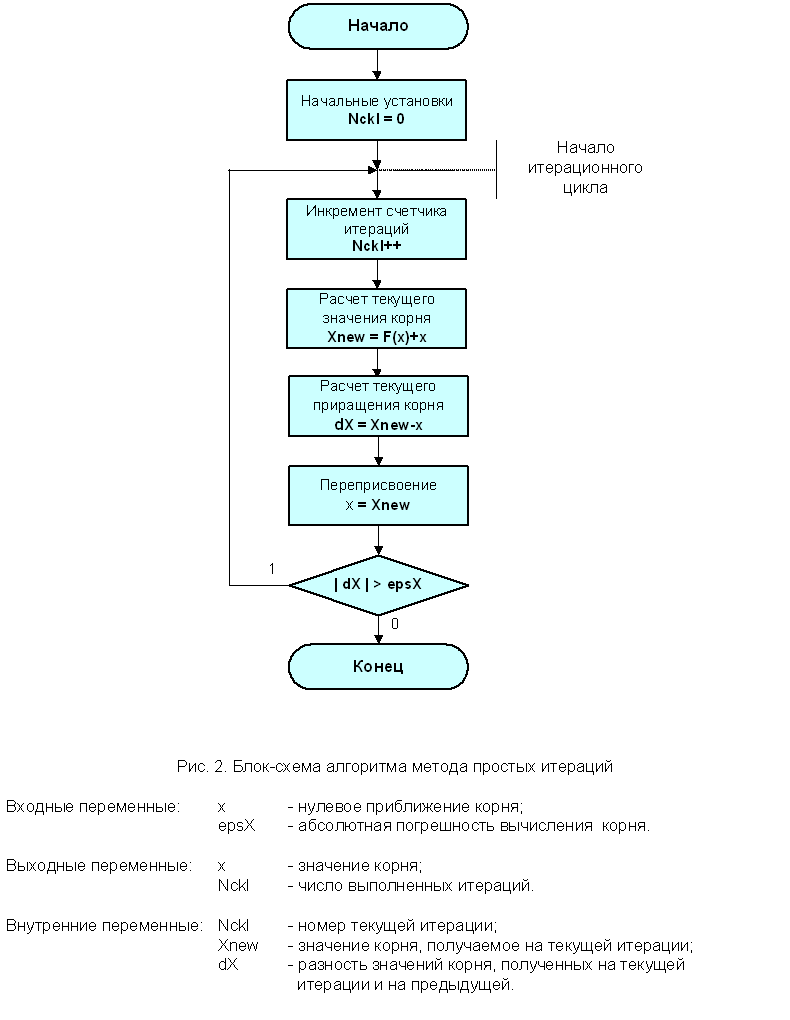 Блок-схема
алгоритма метода простых итераций представлена на рис. 2.
Блок-схема
алгоритма метода простых итераций представлена на рис. 2.
Для некоторых уравнений бывает трудно выбрать нулевое приближение корня. Зато часто можно легко указать интервал, в котором он ожидается
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.