











































равны друг другу, то траектория уже не будет эллипсом, а имеет вид сложной незамкнутой линии. Только, когда частоты колебаний nх и nу отличаются в целое число раз, траектории получаются замкнутыми и называются фигурами Лиссажу.
Форма фигуры Лиссажу позволяет определить отношение частот складываемых колебаний. Для этого достаточно подсчитать число пересечений фигуры с осью X и осью Y. Если ось координат проходит через точку пересечения ветвей фигуры Лиссажу, то эту точку считают дважды.
|
|
Для фигуры Лиссажу, изображенной на рис.2, число пересечений ее ветвей c осью X равно nх = 2, а с осью Y - nу = 4. Можно показать, что отношение частот складываемых колебаний связано с числом пересечений формулой
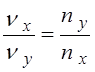 (7)
(7)
|
|
Для примера рис.2 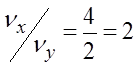 .
.
Эллипс —
простейшая фигура Лиссажу, для которой 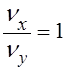 .
.
Пользуясь методом фигур Лиссажу удобно сравнивать частоты колебаний. Например, можно с помощью эталонного генератора градуировать шкалу генератора неизвестных частот.
Для получения фигур Лиссажу собирают схему рис.3. Схема состоит из генератора переменного напряжения ГПН, звукового генератора ЗГ и электронного осциллографа ЭО. Сигналы с ГПН и ЗГ подаются на каналы I и II осциллографа, включенные как отклоняющие луч во взаимно перпендикулярных направлениях.
4. Изучение сложения одинаково направленных колебаний с различными частотами производится также с помощью схемы рис.3. При этом каналы I и II осциллографа включаются так, чтобы оба поступающих на них сигнала отклоняли луч вдоль вертикальной оси у. Включается также генератор развертки ЭО и кнопка сложения сигналов.
Расчет показывает [1], что при одинаковых амплитудах складываемых колебаний
U1 = Uo cos w1t
и
U2 = Uo cos w2t
Суммарное колебание будет определяться выражением
U =
U1 + U2 = 2Uo cos 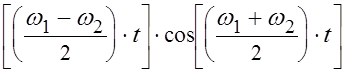 (8)
(8)
Если Dw = w1 - w2 << w1,2 , то есть, если частоты
складываемых колебаний отличаются мало, то колебания (8) называют биениями
(рис.4). Биения приближенно можно рассматривать как гармонические колебания с
циклической частотой 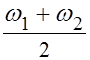 ,
амплитуда которых медленно меняется по закону
,
амплитуда которых медленно меняется по закону
A(t) = 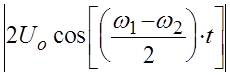 (9)
(9)
Частота
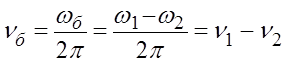 (10)
(10)
называется частотой биений.
Обратная величина
Тб
= ![]() (11)
(11)
является периодом биений.
|
|
Задание
1. Изучить инструкцию по эксплуатации осциллографа, назначение ручек управления.
2. Собрать схему рис.1. Следить, чтобы клеммы «земля» каналов осциллографа ЭО и генератора ЗГ были подключены к общей точке. В качестве реактивного сопротивления Х рекомендуется подключить конденсатор С3. Кнопки управления ЭО «®®» (слева от экрана) и «I» (справа от экрана) должны быть нажаты.
3. Получить на экране одновременно два гармонических сигнала. Меняя частоту ЗГ (грубо и плавно) проследить за изменением разности фаз между колебаниями. Определить, при каких частотах разность фаз равна нулю, а при каких - наибольшая. Определить Dj «макс.». = (j2 - j1) численно, сравнивая сигналы. Измерить амплитуды колебаний при частотах соответствующих Dj = 0 и Dj«макс.».
4. Нажав кнопку «I + II » (слева от экрана) сложить однонаправленные колебания. Установив частоту ЗГ, соответствующую Dj = 0, убедиться, что
Uo = U10 + U20
Установив частоту ЗГ, соответствующую Djмакс , убедиться, что
Uo < U10 + U20.
Измерить Uo. Зная Uo , U10 , U20 вычислить по формуле (4) разность фаз
(j2 - j1). Сравнить полученное значение с измеренным ранее в п.3.
5. Сложить колебания как взаимно перпендикулярные. Для этого, не меняя схемы, нажать кнопку «X - Y» слева от экрана и кнопку «X - Y» справа от экрана. Зарисовать траекторию движения луча на экране ЭО при частотах, соответствующих Dj = 0 и Dj «макс.».
6. Собрать схему рис.3. Установить на ГПН один из диапазонов с неизвестной частотой № 4 ¸ 7. Меняя частоту ЗГ добиться получения на экране, во-первых, эллипса. Сняв показания со шкалы генератора определить неизвестную частоту ГПН. Проградуировать, получая эллипс, остальные диапазоны с неизвестными частотами. Изменяя частоту ЗГ получить фигуру Лиссажу. Пользуясь формулой (7) повторить градуировку на некоторых диапазонах. Убедиться, что результаты совпадают с полученными ранее методом эллипса.. В заключение переключить ГПН на диапазон № 3 и методом эллипса определить точное значение частоты на этом диапазоне.
7. Не меняя схемы измерений и диапазонов ГПН и ЗГ сложить их колебания как однонаправленные. Для этого нажать управляющие кнопки «I + II» - слева от экрана и «I» - справа от экрана. Вращая ручку «Время/Дел.» (грубо - плавно» ЭО и немного изменив частоту ЗГ, добиться устойчивой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.