Определение величины опрокидывающего момента конвертера, страница 3

Продолжение таблицы 2

Первоначально определяется объем металла в ковше. В исходном положении () объем жидкости в ковше будет

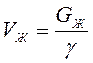,                                                                                                    (14)

где  – вес жидкости в ковше;

– удельный вес жидкости.

Уровень жидкости при вертикальном положении ковша (рисунок 3) определяется из равенства

                                                                                     (15)

Указанные объемы определяются по вышеприведенным формулам и с учетом, что

p                                                                                                (16)

где R – радиус цилиндра;

 – высота жидкости в цилиндрической части.

Тогда неизвестная величина

.                                                                                      (17)

Уровень зеркала жидкости в ковше относительно его основания определится

                                                                                      (18)

Далее вычерчивается внутренний контур ковша в масштабе и проводится уровень зеркала жидкости. При наклоне ковша зеркало жидкости остается горизонтальным, т.е. оно поворачивается относительно ковша на угол . Центром поворота зеркала, до того момента пока оно не достигнет сливного отверстия ковша, является точка пересечения поверхности жидкости с вертикальной осью. После пересечения зеркалом кромки отверстия, ось поворота зеркала переносится на эту кромку. Для нахождения центра тяжести, объема (веса), а затем и момента от веса жидкости, весь объем для заданного угла наклона разбивается на элементарные геометрические фигуры: сегменты, усеченные конусы, цилиндры и шаровые сегменты. Та часть жидкости, которая составляет цилиндрический клин, делится параллельными плоскостями, перпендикулярными к оси ковша. Сложный объем, получаемый в каждом параллельном слое, заменяется сегментным цилиндром. Для этого часть жидкости из нижней зоны слоя перемещается в верхнюю.

Объем и центр тяжести сегментного цилиндра зависит от его центрального угла . Эти параметры удобно определять, используя таблицы, построенные для элементов круга с радиусом равным 1. В таблицах приведены величины единичной площади S, хорды , стрелки С, радиуса R, длины дуги  в зависимости от угла , длины стрелки h. (приложение А).

Графическая иллюстрация методики расчета приведена на рисунке 4.

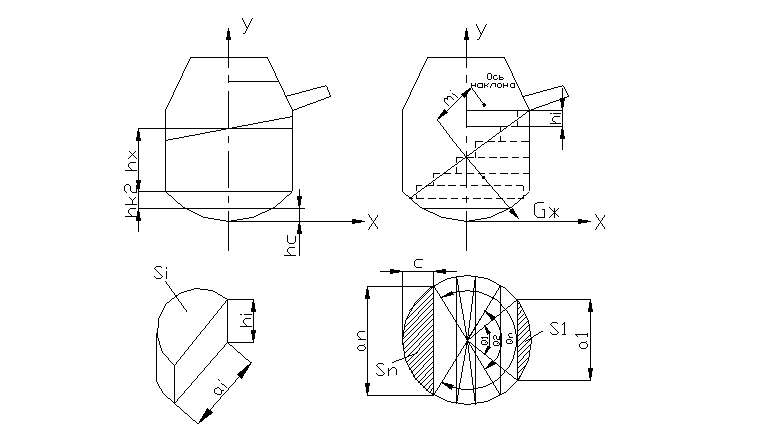
Рисунок 4 – Методика определения центра тяжести жидкости в

зависимости от угла наклона j

Для реальных цилиндрических сегментов при  объем определяется по формуле

.                                                                                                  (19)

Расстояние от оси ковша до центра тяжести сегмента определяется по формуле

.                                                                                                  (20)