Определение величины опрокидывающего момента конвертера, страница 2

Для расчетов нагрузок на механизм опрокидывания ковша по мере его наклона есть несколько способов. В данной работе берется метод П.Н. Аксенова (все остальные методы приведены в работах [1,2].)

Для определения характеристики нагружения механизма опрокидывания нужно полный угол наклона ковша разбить на несколько промежуточных углов (через ,  или ) и просчитать опрокидывающий момент для каждого из этих промежуточных углов. Затем, на основании полученных при расчете данных, построить график изменения величины момента по мере наклона ковша. Это и будет характеристика нагружения механизма опрокидывания ковша.

Опрокидывающий момент, передаваемый от ковша на механизм при его опрокидывании, складывается их 3-х моментов: от веса ковша , от веса жидкости  и от трения в опорах ковша:

.                                                                                   (4)

Определение величин  производим на основании знания параметров модели конвертора, приведенных на рисунке 3.

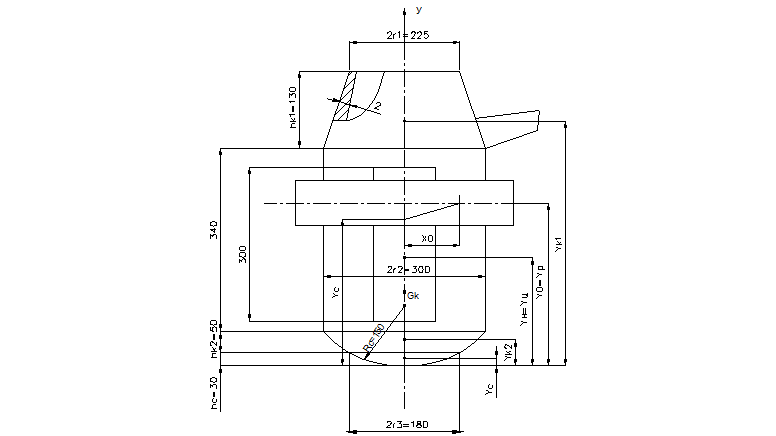
Рисунок 3 – Размеры элементов модели конвертора

Чтобы найти момент от веса ковша, необходимо найти центр его тяжести и плечо приложения веса относительно оси наклона. Пустой ковш вместе с рамой симметричен относительно вертикальной оси (весом носка пренебрегаем), поэтому центр его тяжести лежит на этой оси (рисунок 3). Для нахождения центра тяжести, ковш совместно с рамой, направляющими разбивается на конструктивные элементы простой геометрической формы (цилиндры, усеченные конусы, сферические сегменты, прямоугольники и т. п.). После этого находятся вес и центр тяжести каждого из элементов, а затем по формуле

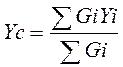                                                                                                  (5)

находится общий центр его тяжести. Веса отдельных элементов установки представляются согласно таблицы 1.

Таблица 1 – Вес элементов ковша

Перечень величин, входящих в таблицу 1:  – вес верхнего конуса;  – вес цилиндрической части;  – вес нижнего конуса;  – вес сферической части;  – вес направляющих;  – вес рамы;  – суммарный вес.

Центр тяжести рамы, направляющих и цилиндрических частей ковша определить легко, они лежат на пересечении диагоналей. А для нахождения центров тяжести оболочек усеченных конусов и сферического сегмента воспользуемся методом отрицательных объемов

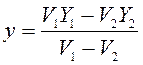.                                                                                             (6)

где  и  – соответственно объем, и центр тяжести фигуры ограниченный наружной поверхностью;

и  – соответственно объем и центр тяжести фигуры, ограниченной внутренней поверхностью.

Для усеченного конуса объем и центр тяжести определяется по формулам

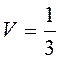p                                                                              (7)

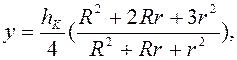                                                                               (8)

где  – высота конуса;

 – большой радиус конуса;

 – меньший радиус конуса.

Для сферического сегмента объем и центр тяжести определяются по формулам

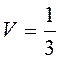p                                                                                    (9)

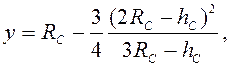                                                                              (10)

где  – высота сферы;

 – радиус сферы.

Данные для расчетов центров тяжести отдельных элементов берутся из рисунка 3.

Рассчитанные центры тяжести отдельных элементов ковша необходимо привести к одной оси (проходящей через основание ковша).

Расстояние от центра тяжести порожнего ковша до оси его наклона

                                                                                 (11)

где  и  – координаты оси опрокидывания ковша (выбираются индивидуально в соответствии с вариантом по таблице 3).

Угол между радиусом-вектором и горизонталью

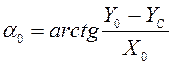.                                                                                      (12)

При заданной координате , принять угол .

Опрокидывающий момент от веса порожнего ковша в функции угла наклона

.                                                                               (13)

Задаваясь значениями угла  – через , находим соответствующие значения опрокидывающих моментов от веса порожнего ковша.

Опрокидывающий момент от веса жидкости ковша для различных углов наклона определяется графоаналитическим методом проф. Н.А. Аксенова.

Таблица 2 – Исходные данные для расчета