




4. РАСЧЕТ НЕДОСТАЮЩИХ ПАРАМЕТРОВ ЭЛЕКТРОДВИГАТЕЛЯ И ПОСТРОЕНИЕ МЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКИ МАШИНЫ В ПРЕДПОЛОГАЕМЫХ ЗОНАХ РАБОТЫ.
Расчет недостающих параметров ведется исходя из необходимости построения механических характеристик (естественной и искусственной ), а также для построения структурной схемы электропривода.
Т.о. необходимо найти зависимость скорости двигателя от приложенного к нему момента. Для короткозамкнутых асинхронных двигателей в области скольжений 1≥s>sк неплохие результаты дает формула К.А. Чекунова
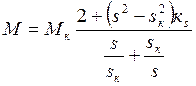 ;
;
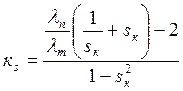 ;
;
где λп, λт – соответственно кратности пускового и максимального моментов;
Mk – критический момент двигателя;
sk – критическое скольжение;
s – скольжение.
Из этих формул видно, что весь расчет для построения естественной механической характеристики сводиться к нахождению sk. Для этого можно представить критическое скольжение в виде:
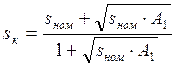 ;
;
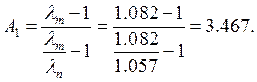
где sном – номинальное скольжение двигателя, которое можно рассчитать по следующей формуле:
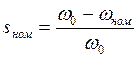 .
.
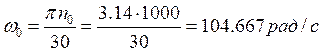 ;
;
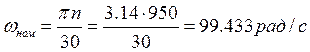 ;
;
где ω0, ωном – соответственно синхронная и номинальная угловые скорости двигателя, рад/с;
n– скорость двигателя, об/мин;
n0– синхронная скорость двигателя, об/мин.
Тогда
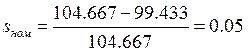 ;
;
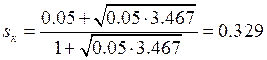 ;
;
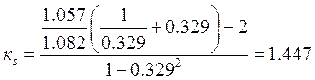 .
.
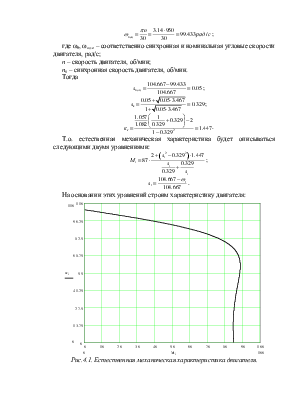
Т.о. естественная механическая характеристика будет описываться следующими двумя уравнениями:
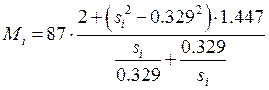 ;
;
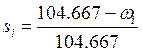 .
.
На основании этих уравнений строим характеристику двигателя:
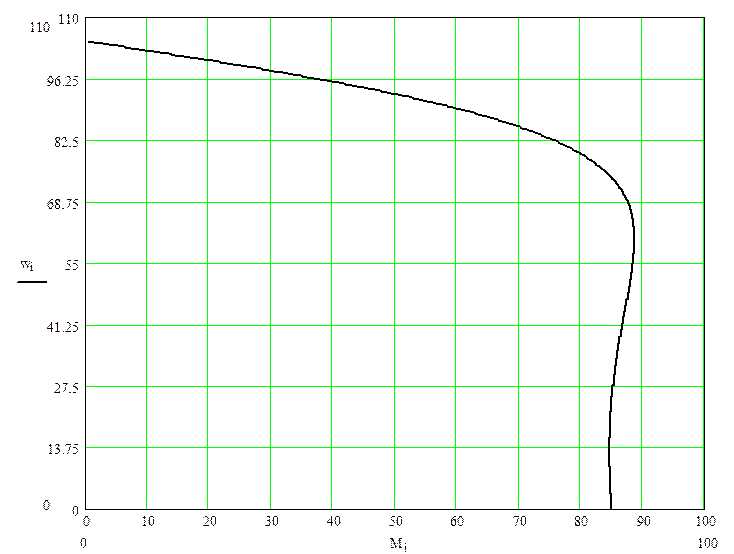
Рис.4.1. Естественная механическая характеристика двигателя.
Но кроме построения естественной механической характеристики нам необходимо построить характеристики для частотного управления скоростью.
Характеристики же, которые будут лежать ниже рабочей, будут являться переходными, т.е. описывающими процесс плавного пуска (торможения) двигателя.
Для того чтобы построить эти характеристики необходимо привести полученную систему из двух уравнений к такому виду, при котором механическая характеристика будет менять свой вид при изменении частоты питающего двигатель напряжения.
Существует ряд способов частотного регулирования. Для нашего электропривода наиболее приемлемым видится способ по закону Фmax=const, где Фmax–максимальный магнитный поток в статоре. При этом законе регулирования значения критического момента и критического скольжения будут постоянными. Здесь будет наблюдаться эффект сдвига оси абсцисс в зависимости от величины частоты относительно оси ординат. Поэтому на основании этого систему описывающую механические характеристики при частотном управлении можно представить в следующем виде:
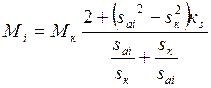 ;
;
![]() ;
;
где ωном – номинальная скорость двигателя;
sai – абсолютное скольжение, которое можно выразить следующим образом:
![]() ;
;
ν – относительная скорость:
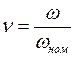 ;
;
α – относительная частота:
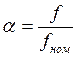 ;
;
fном и f – номинальная (50Гц) и заданная частоты питающего двигатель напряжения.
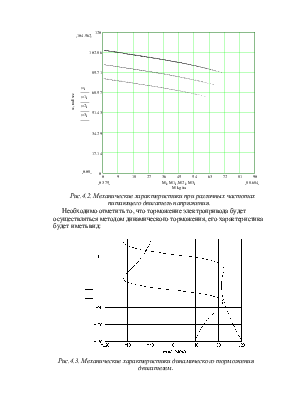
На основании полученной системы уравнений построим механические характеристики при следующих частотах: 49,938Гц, 44,125Гц, 38,43Гц и номинальной 50Гц.
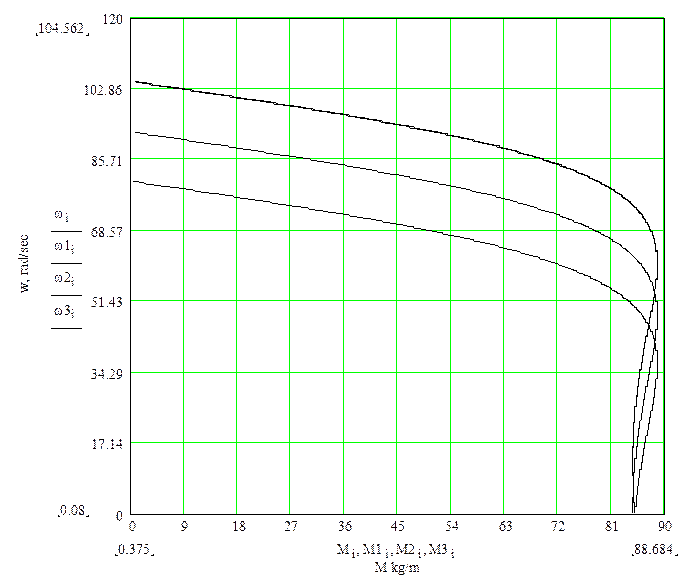
Рис.4.2. Механические характеристики при различных частотах питающего двигатель напряжения.
Необходимо отметить то, что торможение электропривода будет осуществляться методом динамического торможения, его характеристика будет иметь вид:
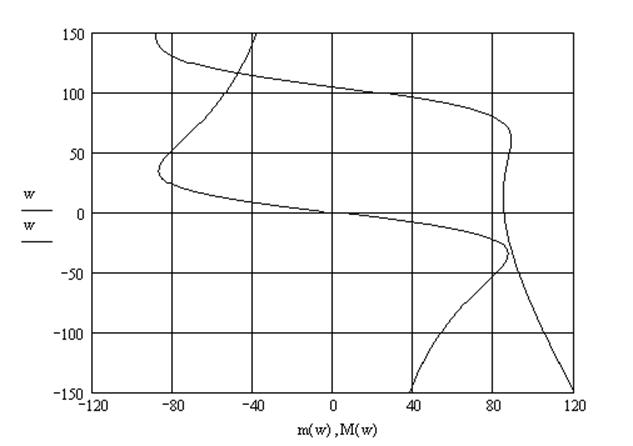
Рис.4.3. Механические характеристики динамического торможения двигателем.
Реализовать схему динамического торможения можно следующим образом:
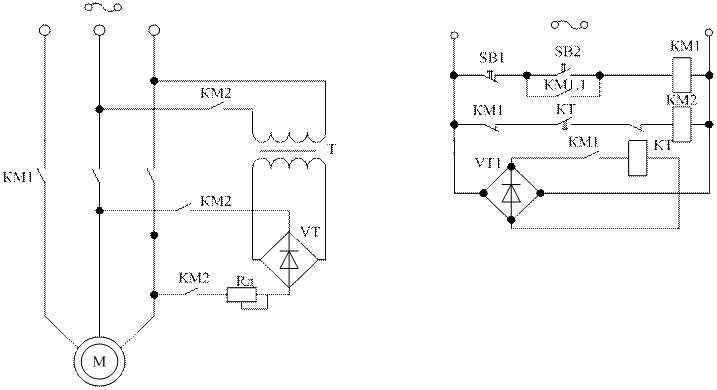
Рис.4.4. Схема динамического торможения асинхронного двигателя.
Найдем теперь параметры необходимые для построения структурной схемы, а также те параметры, которые понадобятся для ее анализа.
Рассчитаем номинальный ток двигателя:
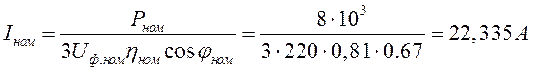 .
.
Полное сопротивление короткого замыкания, Ом:
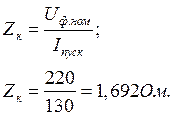
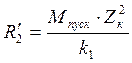 ;
;
где 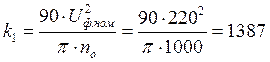 ;
;
nо– скорость идеального холостого хода, об/мин.
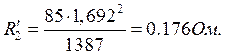
Активное сопротивление фазы статора:
![]() ;
;
где cosφпуск – коэффициент мощности при пуске:
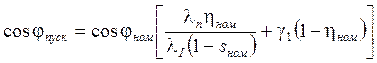 ;
;
где γ1 – отношение мощности потерь мощности в обмотке статора при номинальной нагрузке к полным номинальным потерям, определяемое по формуле:
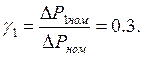
Откуда
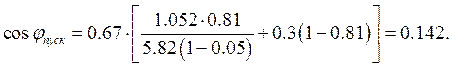
![]()
Индуктивное сопротивление короткого замыкания, Ом:
![]() .
.
Индуктивные сопротивления рассеяния статора и ротора примерно равны:
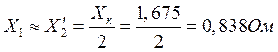 .
.
Ток холостого хода короткозамкнутого асинхронного двигателя :
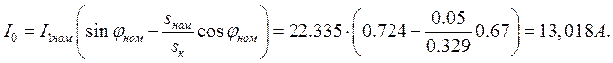
Приведенный ток ротора:
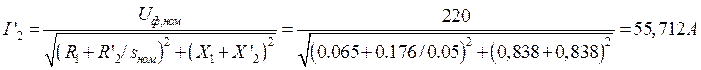 .
.
ΔР0 – потери мощности при холостом ходе, Вт:
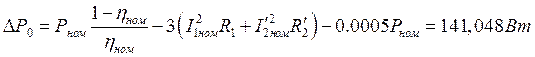
Коэффициент мощности при холостом ходе двигателя:
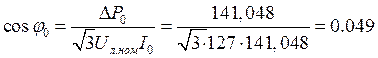 .
.
Индуктивное сопротивление намагничивающего контура:
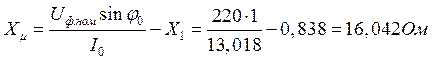 .
.
Активное сопротивление намагничивающего контура:
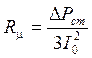 .
.
где ∆Рсm – потери в стали статора Вт, определяемые по формуле:
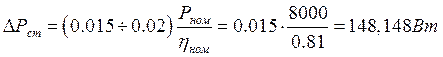 ;
;
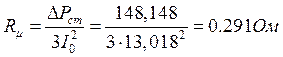 .
.
Электромеханическая постоянная времени электропривода:
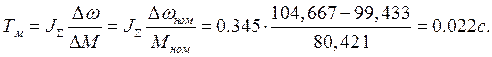
где JΣ – суммарный момент инерции электропривода, кг·м²;
Δωном – падение угловой скорости на данной механической характеристике при изменении электромагнитного момента от нуля до Мном.
Электромагнитная постоянная времени АД, с:
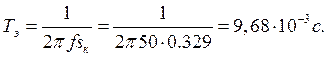
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.