Динамика обобщенной разомкнутой электромеханической системы

демпфирование (l_пред = 2,2) и соответствует значительным Т_э*, в то время как при Т_э* = 0, l_max = 0,85, т. е. ниже в 2,6 раза.

Так как индуктивность диссипативными свойствами не обладает, возможность ее демпфирующего действия требует разъяснений. При малых g и m < 4 система имеет две пары комплексных корней и две резонансные частоты, из которых первая пара и первая частота характеризуют колебательность двигателя, а вторая резонансная частота близка к частоте свободных механических колебаний. При увеличении индуктивности рассеяния колебательность двигателя, зависящая от m = Т_м1 / Т_э, увеличивается и меньший резонансный пик АЧХ возрастает. Однако увеличение колебательности двигателя при малом моменте инерции J₂ увеличивает электромеханическую связь и отвод энергии механических колебаний в цепь якоря; второй резонансный пик, обусловленный параметрами механической части, соответственно уменьшается.

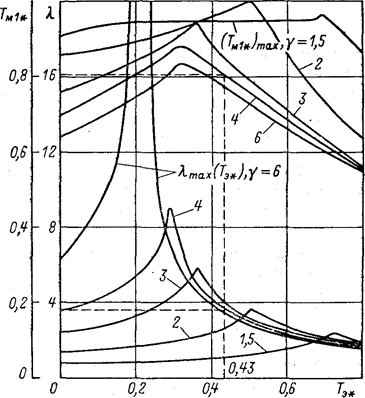
Рис. 4.18. Характеристики максимального демпфирования.

Увеличение индуктивности приводит к уменьшению общей колебательности системы только до того ее значения, при котором наступает равенство резонансных пиков. Дальнейшее увеличение индуктивности вызывает возрастание колебательности. Такие условия наступают тем раньше, чем больше g.

При Т_э* = 0 значения l_max однозначно определяются соотношением масс g. Зависимости l_max = ¦(g) и (T_м*1)_опт = ¦(g) при Т_э* = 0 представлены на рис. 4.19 (кривые 1 и 1'). Они иллюстрируют закономерность, согласно которой в системе без электромагнитной инерции подбором жесткости механической характеристики получить апериодический характер процессов можно только при g ³ 9. При g > 9 критическому демпфированию соответствуют два значения (Т_м1*.)_max и два значения жесткости механической характеристики. Кривая 1' в этой области разветвляется, и заштрихованной зоне соответствуют значения Т_м1*., при которых все корни уравнения (4.37) являются действительными и отрицательными.

Кривые на рис. 4.18 свидетельствуют о том, что варьирование электромагнитной инерционности двигателя позволяет получить при каждом g большее демпфирование, чем при Т_э* = 0. Предельные значения логарифмического декремента, соответствующие каждому g, позволяют построить зависимость l_пред = ¦(g) и соответствующие ей зависимости (Т_м1*)_опт = ¦(g) и (Т_э*)_опт  = ¦(g)  (кривые 2, 2' и 2" на рис. 4.19). Эти кривые показывают, что при наличии электромагнитной инерции Т_э* ¹ 0 критическое демпфирование достигается при g ³ 5,5, т. е. возможности использования демпфирующего действия электропривода в системах с малым приведенным моментом инерции механизма повышаются.

Представленные на рис. 4.18 характеристики дают возможность определять сочетания параметров, оптимальные по демпфированию колебаний в упругой разомкнутой электромеханической системе.

Пример 4.2. Определить оптимальную по критерию минимума колебательности жесткость механической характеристики электропривода постоянного тока, для которого частные параметры электрической и механической частей имеют следующие значения:

kФ_ном=с=2,84 В×с; R_яS=0,098 Ом (в нагретом состоянии машины); Т_я = 0,03 с; J₁ = 3,5 кг×км²; J₂ = 10,5 кг×м²; c₁₂ = 548 Н×м.

Определим обобщенные параметры, соответствующие (4.35):

b = с²/R_яS = 2,84²/0,098 = 82,3 Н×м×с;

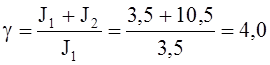
Рис. 4.19. Характеристики предельного демпфирования.

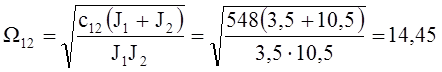1/с

Т_э* = Т_эW₁₂ = 0,03×14,45 = 0,43; (Т_м1*)_е = J₁W₁₂ / b = 3,5×14,45 / 82,3 = 0,61

При g = 4,0 и Т_э* = 0,43 по кривым рис. 4.18 определяем значения l_max и (Т_м1*) _max:

l_max = 3,5; (Т_м1*)_max = 0,805

Модуль оптимальной при Т_э* = 0,43 жесткости механической характеристики

b_max = J₁W₁₂/(Т_м1*)_max3,5×14,45/0,805 = 63 Н×м×с,

Сравнивая b_max c b, можно заключить, что для получения максимального демпфирования при Т_я = 0,03 с жесткость механической характеристики нужно уменьшить на 24%.

Для реализации предельного демпфирования по кривым