У залежнасці ад тыпу палінома адрозніваюць фільтры Батэрворта, Чабышова, Беселя ці крытычны. Крытычным называюць фільтр з характарыстыкай па (3.38) пры a1 = a2 = … = an. У залежнасці ад тыпу фільтра змяняецца выгляд АЧХ і пераходнай характарыстыкі. АЧХ фільтра Батэрворта мае доўгі гарызантальны ўчастак і рэзка спадае за частатой зрэзу. АЧХ фільтра Чабышова больш крута спадае за частатой зрэзу, але ў паласе празрыстасці фільтр мае хвалісты характар з пастаяннай амплітудай ваганняў. АЧХ фільтра Беселя спадае больш паката, аднак пераходная характарыстыка без ваганняў з вялікай хуткасцю ўстанаўлення. Пераходная характарыстыка фільтра Батэрворта мае ваганні і больш вялікі час устанаўлення, фільтр Чабышова мае максімальныя ваганні. З павелічэннем парадку фільтра ваганні і час устанаўлення таксама павялічваюцца. АЧХ і пераходныя характарыстыкі некаторых ФНЧ вышэйшых парадкаў адлюстраваны на мал. 42.
На адной схеме можна атрымаць характарыстыкі любога з тыпаў фільтраў шляхам замены наміналаў рэзістараў і кандэнсатараў, для чаго патрэбна падабраць гэтыя наміналы пад каэфіцыенты ў (3.37)–(3.39).
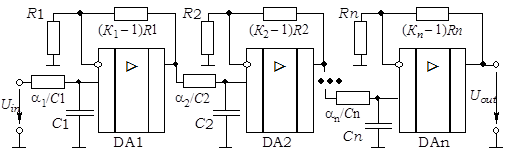
Мал. 40. Прынцыповая схема фільтра n-га парадку на ФНЧ першага парадку
|
Мал. 42. АЧХ і пераходныя характарыстыкі ФНЧ вышэйшых парадкаў: 1, 2, 3, 4 – фільтры Беселя, Батэрворта і Чабышова першага і другога роду адпаведна: а) АЧХ ФНЧ дзесятага парадку; б) АЧХ ФНЧ чацвёртага парадку; в) пераходныя характарыстыкі ФНЧ дзесятага парадку; д) пераходныя характарыстыкі ФНЧ чацвёртага парадку |
17. Фильтры 2-го порядка
Зробім вывад перадатачнай характарыстыкі для актыўнага ФНЧ другога парадку на мал. 41а. Для гэтага з выкарыстаннем адлюстраванняў па Лапласу складзём па метадзе вузлавых патэнцыялаў сістэму ўраўненняў для вузла паміж R1, R2, R3 і C1 і вузла каля інверсавальнага ўваходу з улікам «віртуальнай» зямлі на гэтым уваходзе:
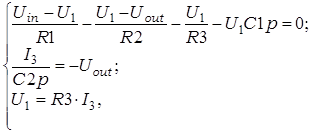(3.40)
дзе U1 – напружанне для вузла паміж R1, R2, R3 і C1. З (3.40) пасля кароткіх пераўтварэнняў атрымаем
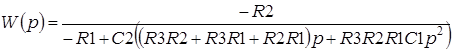. (3.41)
Такім чынам, фільтр на мал. 41а з’яўляецца фільтрам другога парадку.
ФНЧ другога парадку на мал. 41б акрамя дадатнай зваротнай сувязі ўтрымлівае і адмоўную зваротную сувязь, таму выніковая зваротная сувязь аказваецца адмоўнай. Для гэтага каэфіцыент узмацнення, які задаецца адмоўнай сувяззю, павінен быць не вельмі вялікі (блізкі да 1), у іншым выпадку схема становіцца няўстойлівай і пераўтвараецца ў генератар. Пры разліку фільтра можна лічыць, што розніца напружанняў паміж уваходамі роўна нулю, а АУ з ланцугом зваротнай сувязі з’яўляецца неінверсавальным узмацняльнікам з каэфіцыентам узмацнення a. З выкарыстаннем адлюстраванняў па Лапласу складзём па метадзе вузлавых патэнцыялаў сістэму ўраўненняў для вузла 1 і вузла каля неінверсавальнага ўваходу:
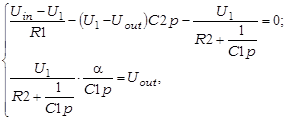(3.42)
дзе U1 – напружанне вузла 1. З (3.42) атрымаем перадатачную характарыстыку фільтра ў выглядзе
. (3.43)
Ад ФНЧ да ФВЧ можна перайсці пры дапамозе лагарыфмічнага прадстаўлення, адлюстраваўшы АЧХ адносна частаты зрэзу. Пры гэтым апошняя застаецца нязменнай, р мяняецца на 1/р, а K0 на K¥ (модуль каэфіцыента ўзмацнення на бясконца вялікай частаце). Перадатачная характарыстыка для ФВЧ пры такіх пераўтварэннях прымае выгляд
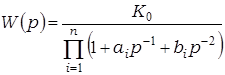, (3.44)
а на прынцыповай схеме для ФНЧ кандэнсатары і рэзістары мяняюцца месцамі, што дазваляе выкарыстоўваць для ФВЧ усе разгледжаныя схемы для ФНЧ. Пры гэтым захоўваюцца і метады разліку характарыстык. Пераходная характарыстыка ФВЧ у адрозненне ад ФНЧ мае ваганні для ўсіх тыпаў фільтраў, АЧХ ФВЧ з’яўляецца адлюстраваннем АЧХ ФНЧ пры замене wRC на 1/wRC.
Перадатачная характарыстыка паласавога фільтра атрымліваецца з ФНЧ заменай р на (1/DW)/(p + 1/p), дзе DW = Dw/w0 – нармаваная шырыня паласы прапускання. Пры такім пераўтварэнні АЧХ ФНЧ зрушваецца ў вобласць высокіх частот на велічыню DW/2. Пасля гэтага выніковая АЧХ паўтарае зрушаную характарыстыку пры w ³ w0, адначасова зрушаная характарыстыка ФНЧ адлюстроўваецца адносна лініі w = w0 у лагарыфмічным маштабе і пераўтвараецца ў зрушаную характарыстыку ФВЧ, якую паўтарае выніковая АЧХ пры w < w0. Перадатачная характарыстыка паласавога фільтра з’яўляецца функцыяй другога парадку, а сам паласавы фільтр выконваецца ў выглядзе паслядоўнага злучэння ФНЧ і ФВЧ, частоты зрэзу якіх у агульным выпадку адрозніваюцца. Для паласавога фільтра можна выкарыстоўваць таксама і схемы ФНЧ другога парадку на адным АУ, калі памяняць месцамі адну пару R, C. Пры гэтым метады разліку перадатачных характарыстык захоўваюцца.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
