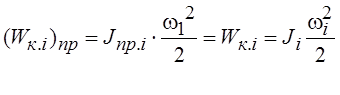
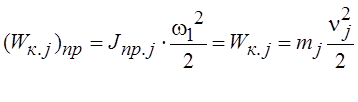
Отсюда формулы приведения принимают вид
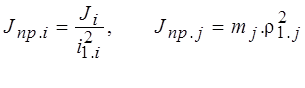 , где i1.i = ω1 / ωi
- передаточное число кинематики от вала двигателя до i-того
ее элемента, ρ1.j = νj / ω1 – радиус
приведения к валу со скоростью ω1.
, где i1.i = ω1 / ωi
- передаточное число кинематики от вала двигателя до i-того
ее элемента, ρ1.j = νj / ω1 – радиус
приведения к валу со скоростью ω1.
В линейных кинематических передачах передаточное число и радиус приведения постоянны. При приведении жесткостей механических связей должно выполняться условие равенства запаса потенциальной энергии деформации. Тогда
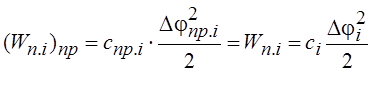 ,
,
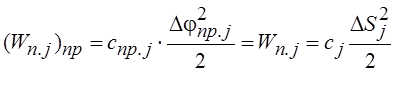 .
.
Из приведенных выражений получаются формулы приведения для жесткостей:
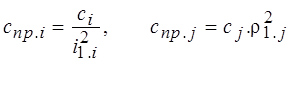 .
.
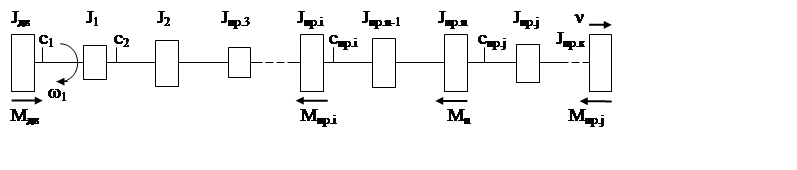 Таким образом, расчетная схема электропривода примет вид:
Таким образом, расчетная схема электропривода примет вид:
Рис. 7
Исследования электромеханических систем показывают, что неразветвленные расчетные механические схемы в результате выделения главных масс и жесткостей сводятся или к трехмассовой или двухмассовой или к жесткому приведенному механическому звену (одномассовой системе). Трехмассовая расчетная схема представлена на рис. 8.
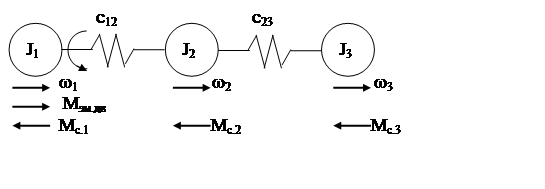
Рис. 8
Здесь первая масса – это ротор (якорь) двигателя и жестко с ним связанные элементы. К этой массе приложен электромагнитный момент двигателя Mэм.дв и момент статической нагрузки Mс.1 – это потери на валу двигателя (механические, вентиляционные и т. п.). Вторая масса – это масса кинематических звеньев, к которой приложен момент сопротивления Mс.2. Третья масса – это масса механизма, технологической машины, к которой приложен момент внешних сил, внешней нагрузки.
Для исследования отдельных физических особенностей электромеханической системы трехмассовая система сводится к двухмассовой системе, рис. 9.
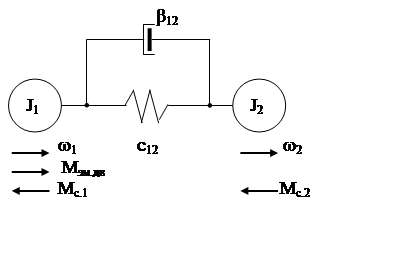
Рис. 9
Первая масса – это суммарный приведенный момент инерции элементов, жестко связанных с валом двигателя. Суммарный приведенный момент инерции элементов, жестко связанных с рабочим органом механизма, характеризуется J2 . Безинерционная связь между этими двумя массами c12. Мс.1 и Мс.2 – это суммарные моменты нагрузки. β12 – это коэффициент, характеризующий влияние люфтов и зазоров.
В тех случаях, когда состояние системы таково, что влияние упругих связей, люфтов и зазоров незначительно, то механическая часть электропривода представляется одномассовой системой, рис. 10.
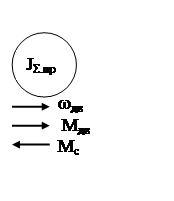
Рис. 10
Здесь JΣ.пр – суммарный приведенный момент инерции электропривода (электромеханической системы):
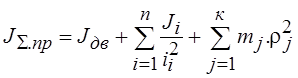
Суммарный приведенный к валу двигателя момент статической нагрузки Мс
в общем можно записать
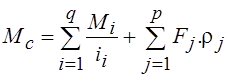 , где q и p – число внешних моментов и сил, приложенных к
системе, кроме электромагнитного момента двигателя.
, где q и p – число внешних моментов и сил, приложенных к
системе, кроме электромагнитного момента двигателя.
При наличии в механизме нелинейной кинематической передачи вычисление приведенного момента сопротивления механизма и момента его инерции выполняется по другим выражениям. Приведем обобщенную нелинейную кинематическую передачу, рис 11. Такого рода механизм имеют резальные машины, пресса для обжатия пакетов бумаги и т. п.
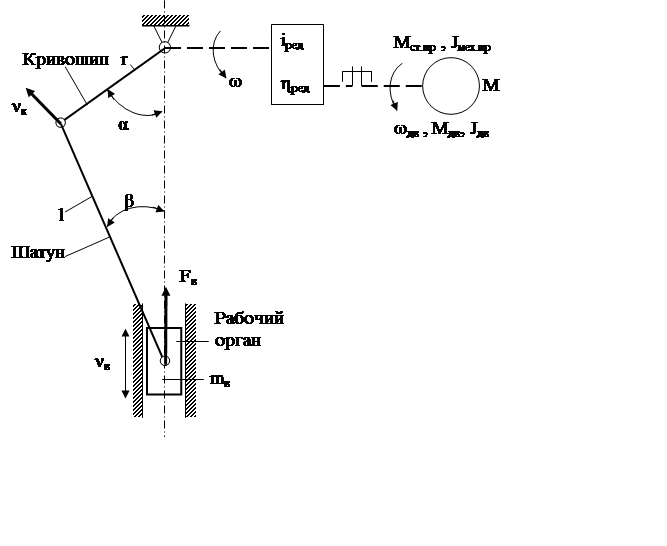
Рис. 11.
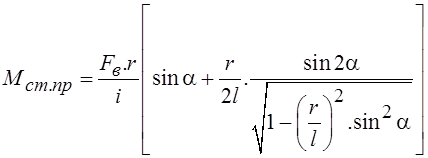 ,
,
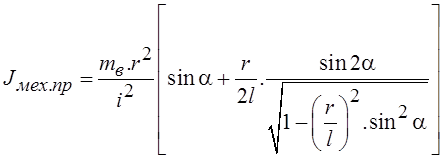 , т. е. эти величины являются функцией угла поворота
кривошипа. Выражение для определения момента получено без учета потерь энергии
в кинематических элементах и передачах. В практических расчетах следует
произвести анализ соотношений размеров кривошипа и шатуна (ползуна). Если
, т. е. эти величины являются функцией угла поворота
кривошипа. Выражение для определения момента получено без учета потерь энергии
в кинематических элементах и передачах. В практических расчетах следует
произвести анализ соотношений размеров кривошипа и шатуна (ползуна). Если 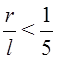 , то угол β можно положить равным нулю
из-за его малого значения. И тогда значение приведенного момента статического
сопротивления механизма с кривошипно-шатунным механизмом вычисляется по формуле
, то угол β можно положить равным нулю
из-за его малого значения. И тогда значение приведенного момента статического
сопротивления механизма с кривошипно-шатунным механизмом вычисляется по формуле
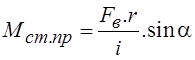 .
.
В большинстве случаев значение момента инерции кинематических передач, но следует учитывать в оценке общей инерционности механической части электромеханической системы. Практика подсказывает, что эту оценку целесообразно проводить относительно момента инерции якоря (ротора) приводного электродвигателя. Количественно это составляет от 10% до 30% его момента инерции. Таким образом, суммарный приведенный момент инерции механической части электропривода выражается следующей формулой
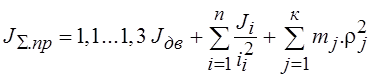 , или
, или
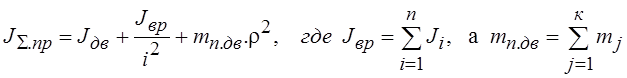 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.