![]()
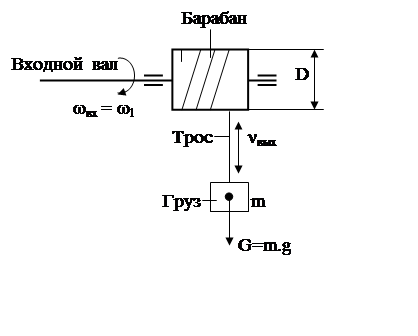
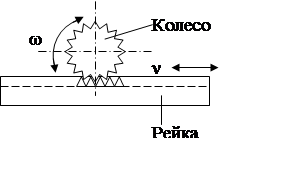
Рис. 3.
Такие кинематические передачи характеризуются таким параметром как радиус приведения
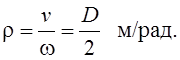
Алогичное преобразование предыдущему выполняют такие кинематические передачи как винтовая и червячная пары, рис. 4.
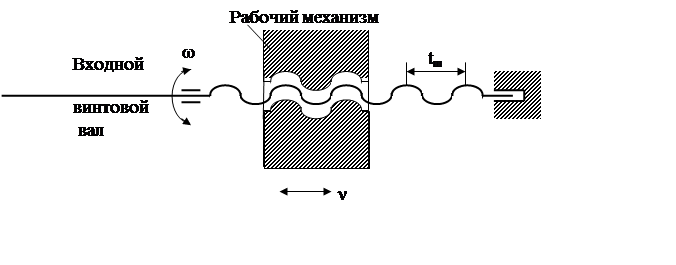
Рис. 4.
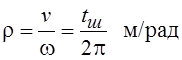 ,
,где tш – шаг винтового вала.
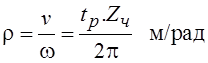 ,
,где tр – шаг червяка, рейки, Zш – число заходов червяка.
Нелинейной по определению кинематической передачей является кривошипно-шатунный механизм. Он преобразует вращательное движение (кривошипа) в поступательное движение (ползуна). Схематический вид таких передач приведен на рис. 5.
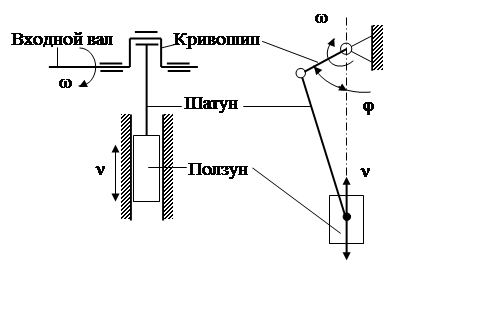
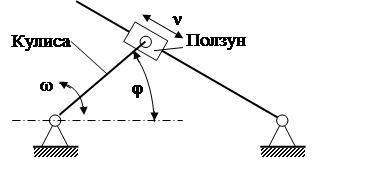
Рис. 5
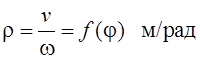 .
.Кинематические передачи конкретного производственного механизма, в частности полиграфического оборудования, могут включать различные рассмотренные выше кинематические звенья, и поэтому они многообразны. В качестве примера на рис. 6 приведена механическая часть электромеханической системы обобщенного типа. Движение любого элемента как материального тела можно описать на основании второго закона Ньютона:
для вращающегося вокруг неподвижной оси
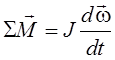 , для поступательного движущегося
, для поступательного движущегося
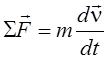 .
.
Здесь ![]() – векторы суммы моментов или сил,
действующих на тело, J и m – момент инерции и масса тела,
– векторы суммы моментов или сил,
действующих на тело, J и m – момент инерции и масса тела, ![]() – угловое ускорение,
– угловое ускорение, ![]() – линейное ускорение. Из приведенной схемы
видно, что каждый вращательно движущийся элемент имеет момент инерции Ji
и связан со следующим вращающимся элементом механической связью, обладающей
жесткостью сi. Каждый поступательно движущий элемент имеет массу mj и связан со следующим элементом механической
связью с жесткостью cj. Для подавляющего
числа упругих механических связей выполняется закон Гука, согласно которому их
жесткости определяются следующими соотношениями:
– линейное ускорение. Из приведенной схемы
видно, что каждый вращательно движущийся элемент имеет момент инерции Ji
и связан со следующим вращающимся элементом механической связью, обладающей
жесткостью сi. Каждый поступательно движущий элемент имеет массу mj и связан со следующим элементом механической
связью с жесткостью cj. Для подавляющего
числа упругих механических связей выполняется закон Гука, согласно которому их
жесткости определяются следующими соотношениями:
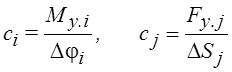 , Mу.i и Fу.j –
, Mу.i и Fу.j –
где Mу.i и Fу.j – момент или усилие нагружающие упругую механическую связь,
Δφi и ΔSj – деформации упругого звена при вращательном и поступательном движении.
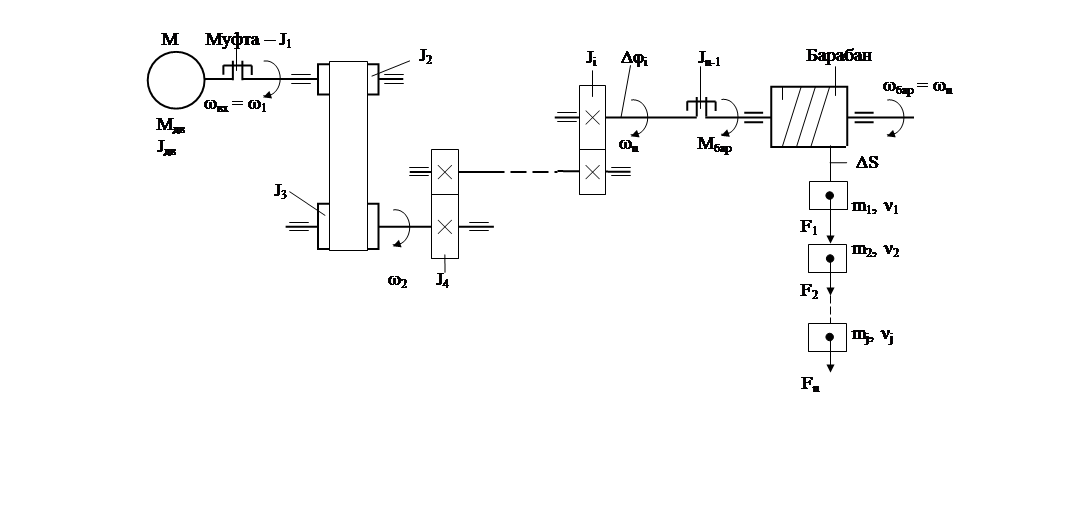
Рис. 6
Для изучения такой многомассовой системы, в которой имеются тела, обладающие отличными друг от друга моментами инерции, массой, скоростью, жесткостью, угловым и линейным перемещениям, необходимо составить для скорости каждой массы уравнения движения, а затем их совместно решить. Это превращается в очень сложную задачу. Поэтому целесообразно было бы иметь схему механической части такой, у которой бы все элементы двигались с одинаковой скорость, т.е. реальную схему заменить на расчетную и привести все параметры к расчетной схеме, а в основу этой схемы положить элемент, движение которого и следовало бы рассмотреть. В электромеханической системе типа электропривода за таковой элемент принимают вал электродвигателя, с которого снимается механическая энергия, а скорость этого вала и будет расчетной. Таким образом, при составлении расчетной схемы выполняется процедура приведения всех параметров к скорости вращения вала электродвигателя, а в основу приведения для создания энергетически эквивалентной схемы закладывают выполнение закона сохранения энергии, как кинетической, так и потенциальной всех элементов системы, а также элементарной работы всех действующих в системе сил и моментов на всевозможных перемещениях.
В зависимости от задач изучения электромеханических систем выбирается любой другой ее элемент, например, промежуточный вал редуктора или исполнительный орган или т. п.
При составлении расчетной схемы следует обратить внимание на то, какие тела оказывают определяющее влияние на движение электромеханической системы, а это — наибольшие массы и наименьшие жесткости механических связей. В соответствии с условием получения расчетной схемы приведение момента инерции элемента системы, движущегося со скоростью ωi, или массы, поступательно движущейся тела со скоростью νj, будут справедливы следующие соотношения для кинематической энергии:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.