Другие предметы \ Автоматизация технологических процессов отрасли

Расчет параметров регулятора локальной и каскадной системе регулирования. Разработка подходов по реализации воздействия от регулятора для регулирования расхода воды, страница 2

Рис.2

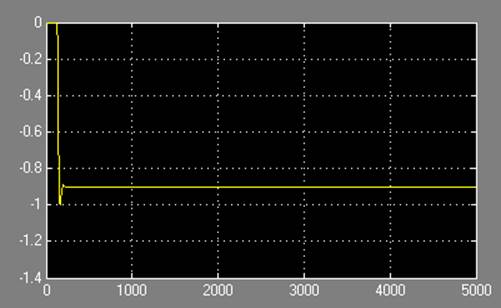
Рис.3

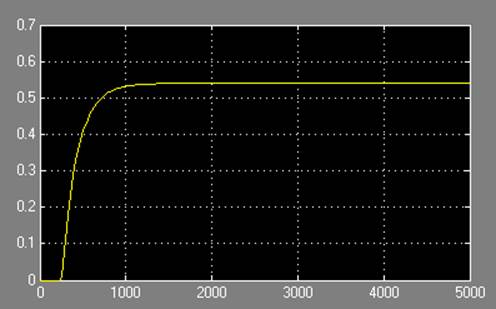
Рис.4

Далее преобразуем схему следующим образом:

Расчет каскадного контура произведем на желаемую степень колебательности М = 1,1.

С учетом      получим:

clc, clf, clear;

ww=tf([-0.9], [80 10 1], 'td', 64);

figure(1);

nyquist(ww);

M=1.1;

w=0:0.001:2;

kp=-1.63;

Tpd=-0.0001;

p=j*w;

www=(kp.*1+Tpd./p)*(-0.6).*exp(-114.5*p)./(80*p.^1+10*p+1);

Re=real(www);

Im=imag(www);

R=M/(1-M^2);

p=j*w;

C=M^2/(1-M^2);

x=-1:0.005:0;

y1=sqrt(R^2-(x-C).^2);

y2=-sqrt(R^2-(x-C).^2);

k=tan(asin(1/M));

y3=k*x;

figure(2);

plot(Re, Im, x, y1, 'r', x, y2, 'r', x, y3);

grid on;В результате вычислений получим следующие результаты:

Принимаем :

Kp=-1.63

Ti=-0,0001

Отсюда следует, что нам необходимо использовать ПИ регулятор.

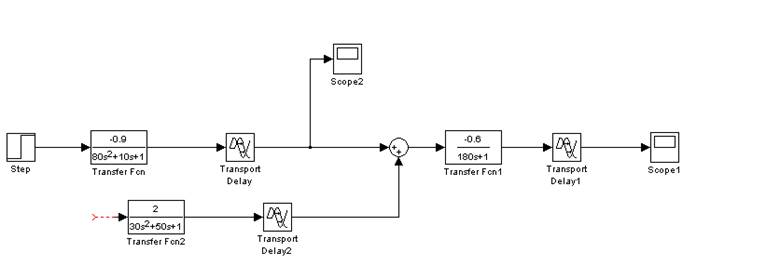
Рис.5 Проверка устойчивости системы без регулятора

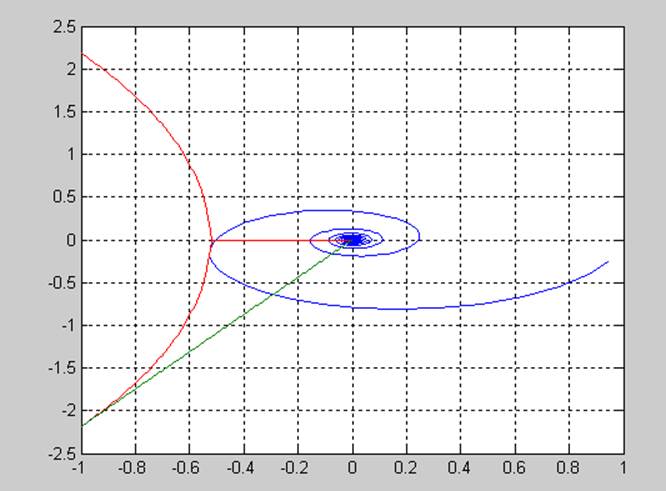
Рис.6

Теперь промоделируем систему с регулятором рисунок 7.

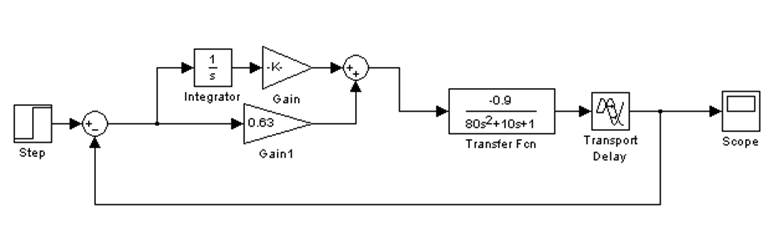
Рис.7

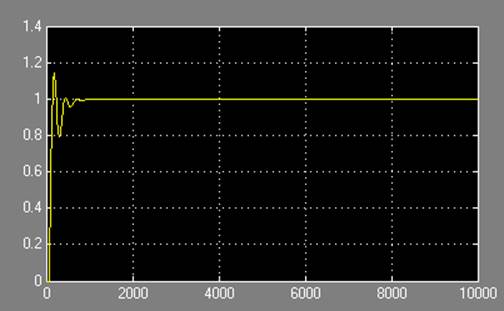
Рис.8

Переходный процесс системы с ПИ-регулятором

Далее преобразуем схему следующим образом:

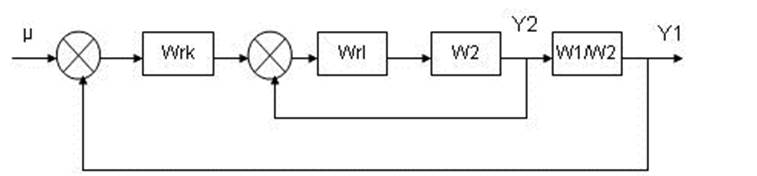
Презентация1

Рис.9

Расчет каскадного контура произведем на желаемую степень колебательности М = 1,1.

С учетом      получим:

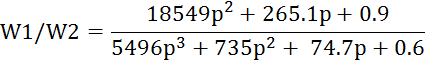
w1=w11*w222;

w12=w1/w2

wr=tf([-0.63 -0.0001],[1 0])

%Ws=wr*w2*w12

ws=((w2*wr)/(1+w2*wr))*w12

[g v]=tfdata(w12,'g')

nyquist(ws)

M=1.1

w=-2.5:0.0005:2.5;

s=i*w;

Kp=-1.4; Ti=0;

Td=-0.001

W=(Kp+Td.*s+1/ Ti.*s).*(( 1.445e008*s.^6 + 4.153e006*s.^5 + 4.418e004*s.^4 + 207.3*s.^3 + 0.372*s.^2 + 5.4*s+0)./(2.335e012*s.^9 + 3.789e011*s.^8 + 4.14e010*s.^7 + 1.265e019*s.^6 + 1.795e007*s.^5 + 1.349e005*s.^4 + 525.2*s.^3 +0.8419*s.^2+3.6*s));

re=real(W); im=imag(W);

R=M/(1-M^2);

C=(M^2)/(1-M^2);

y1=sqrt(R^2-(w-C).^2);

y2=-sqrt(R^2-(w-C).^2);

k=tan(asin(1/M));

y3=k*w;

figure(2);

plot(re,im,w,y1,w,y2,w,y3), grid

xlabel('Re')

ylabel('Im')

В результате вычисления получим:

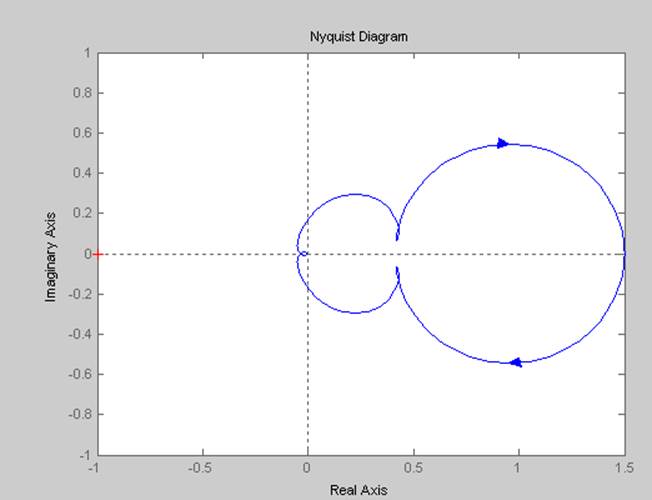
Рисунок 10.  Проверка устойчивости системы без регулятора

,

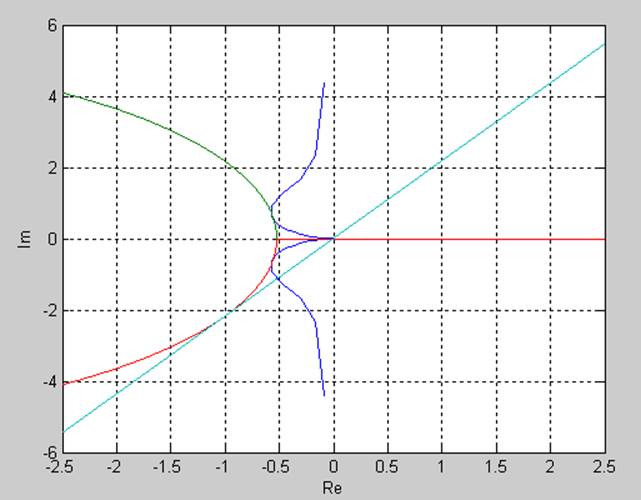
При подборе настроек регулятора, получим (рис 11):

Теперь промоделируем систему в пакете Matlab Simulink (Рис 12):

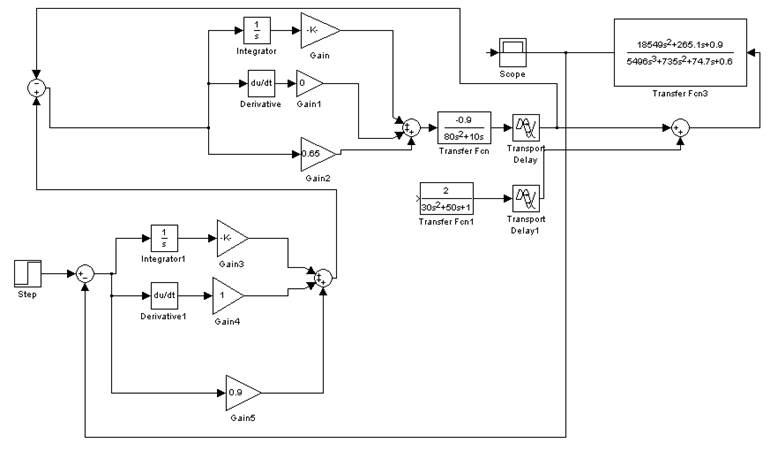
Рисунок 12. Модель каскадной системы

В результате моделирования получим переходный процесс (рис 13):

Определение параметров качества переходных характеристик:

clc, clear

kp=0.05; kd=0.1; kp2=-0.9; ki2=-0.0022; kp=-0.09; kd=-0.0022;

sum('kask1')

% поиск интегральных ошибок

A1=trapz(yy(:,1),(1-yy(:,3)).^2);

A2=trapz(yy(:,1),(1-yy(:,2)).^2);

A3=trapz(yy(:,1),(1-yy(:,4)).^2);

B1=trapz(yy(:,1),abs(1-yy(:,3)).*yy(:,1).^2);

B2=trapz(yy(:,1),abs(1-yy(:,2)).*yy(:,1).^2);

B3=trapz(yy(:,1),abs(1-yy(:,4)).*yy(:,1).^2);

% Перерегулирование

M1=max((yy(:,3)))

M2=max((yy(:,4)))

i=length(yy(:,1));

while abs((1-yy(i,3)))<0.03,

i=i-1;

end

% k=(yy(i+1.3)-yy(i,3))/(yy(i+1.1)-yy(i,1));

% b=abs(1-yy(i,3))-k*yy(i,1); tp1=(0.03-b)/k

% i=length(yy(:,1));

% while abs(1-yy(i,4))<0.03

%     i=i-1

% end

% k=(yy(i+1.4)-yy(i,4))/(yy(i+1.1)-yy(i,1));

% b=abs(1-yy(i,4))-k*yy(i,1); tp2=(0.03-b)/k

figure(1)

plot(yy(:,1),yy(:,2),yy(:,1),yy(:,3),yy(:,1),yy(:,4));grid

% Среднеквадратичное отклонение

[A1/A2 A2/A2 A3/A2]

% % Относительное изменение интегрального критерия

[B1/B2 B2/B2 B3/B2]

[M1 M2]

M1 = 1.1262

M2 = 1.1373

[A1/A2 A2/A2 A3/A2]

ans = 0.0634    1.0000    0.0593

[B1/B2 B2/B2 B3/B2]

ans = 0.0390    1.0000    0.0211

Расчет компенсатора для локальной системы управления

На работу всех систем автоматического управления оказывают влияние непрерывно меняющиеся внешние условия, параметры самой системы и другие факторы. В этом случае стоит задача нейтрализации возмущающих воздействий. Обычно эту задачу решают путем введения второго, компенсирующего возмущение канала и отысканием параметров компенсатора.

Рассмотрим структурную схему заданной системы (рис.16). Система будет полностью инвариантна, если компенсирующее звено Wk(р)  нейтрализует заданное возмущение .

=

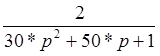
Рассчитаем компенсатор:

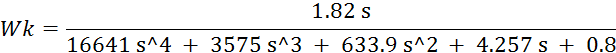
Промоделируем систему:

Рисунок 14

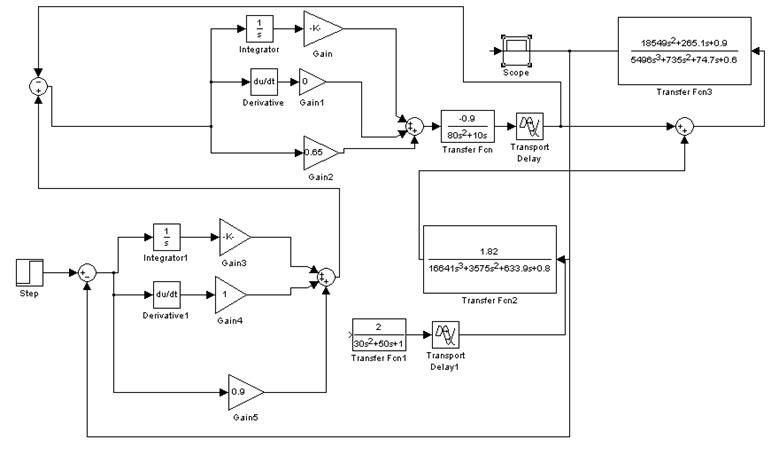
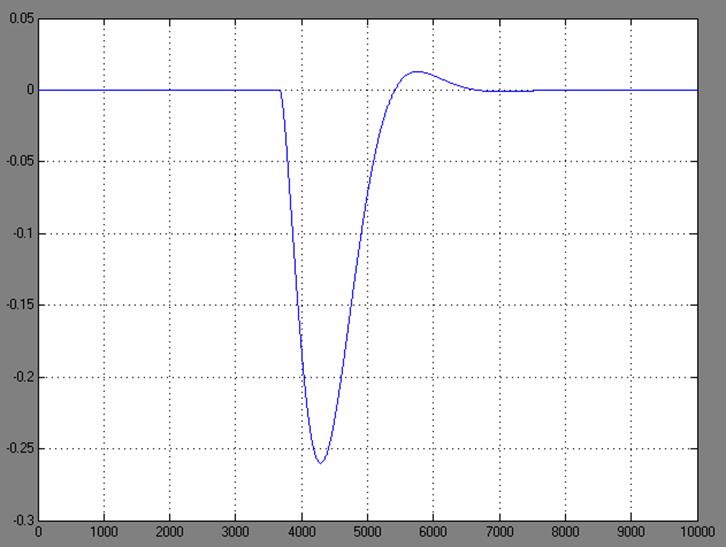
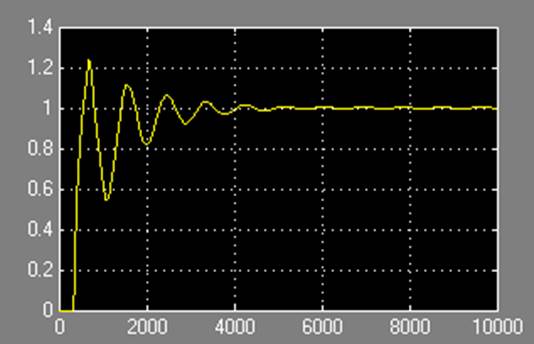
Рисунок 15

По полученным результатам видно, что после воздействия на систему возмущения, компенсатор Wk(р) возвращает ее к исходному состоянию с меньшей погрешностью, чем без компенсатора, следовательно, разработанный компенсатор подходит к данной системе.


Задание 3

Разработать два подхода по реализации воздействия от регулятора для регулирования расхода воды с параметрами: максимальный расход Qmax=25м3/ч; минимальный расход Qm=20м3/ч; номинальный расход Qn=10м3/ч; перепад давления в линии при максимальном значении расхода ΔРL=5.5кгс/см2; температура воды Т=90оС; логарифмически-линейная расходная характеристика.

Скачать файл