



2.4.Математическая модель процесса по необходимым каналам управления,
расчет коэффициентов передаточной функции модели
Математическая модель системы или процесса отражает в той или иной мере свойства реальной системы, в том числе ограничения, существующие в реальных условиях. Математическая модель составляется (разрабатывается) в математических терминах (на математическом языке) и имеет, как правило, количественное описание.
Каждая исследуемая система имеет m входных величин и n выходных величин. Между входными и выходными величинами существуют внутренние динамические связи, вид которых определяется соответствующими динамическими характеристиками.
Реактор каталитического окисления аммиака с точки зрения объекта регулирования можно представить в виде следующей модели:

В качестве выходного параметра реактора используется концентрация нитрозных газов, непосредственно по которой судят о важнейшем показателе процесса – степени конверсии аммиака. Управляющими сигналами являются объемные расходы реагентов в реактор (аммиака и воздуха соответственно). Наиболее типичными возмущениями процесса окисления являются изменение температуры катализаторных сеток реактора, а также колебание расхода по самому платиновому катализатору.
Реактор каталитического окисления довольно специфичен с точки зрения управления. Для разработки математической модели процесса необходимо учесть, что в данном объекте регулирования по каналу соотношение расходов аммиака и воздуха – концентрация нитрозных газов динамика процесса с достаточной точностью аппроксимируется моделью идеального вытеснения, для которой характерно равенство концентраций в сечениях, перпендикулярных движению потока.
С точки зрения физики процесса окисления данная аппроксимация также приемлема. Реакция каталитического окисления аммиака происходит практически мгновенно, в то время как сам реактор по указанному каналу характеризуется некоторой постоянной времени.
Таким образом, передаточная функция реактора по каналу соотношение расходов – концентрация нитрозных газов получается из решения уравнения материального баланса модели идеального вытеснения.
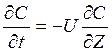
![]()
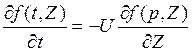
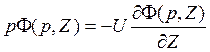
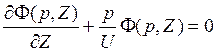
Решение данного дифференциального уравнения 1-го порядка имеет следующий вид:
![]()
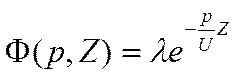
С учетом начальных и граничных условий получаем:
![]()
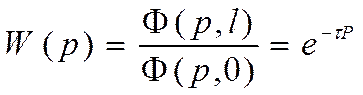
В этом случае динамика системы управления полностью определяется динамическими характеристиками средств измерения и регулирования. С учетом этого, получаем:
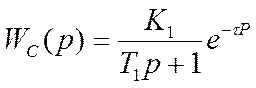
Температура катализаторных сеток – также является одним из важнейших параметров процесса, от значения которого во многом зависят основные показатели процесса окисления. Передаточная функция реактора по каналу соотношение расходов реагентов – температура катализатора определяется из уравнения теплового баланса. Динамика изменения температуры в реакторе с изменением расходов реагентов носит апериодический характер, с коэффициентом усиления и постоянной времени, определяемых из условия ведения технологического процесса.
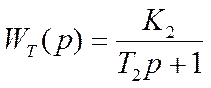
Определим неизвестные величины полученных передаточных функций:
Постоянная времени реактора по каналу температуры Т1 составит:
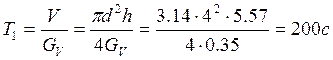 , где d – диаметр реактора;
, где d – диаметр реактора;
h – высота реактора;
GV – объемный расход смеси.
Коэффициент усиления определяется из соображения:
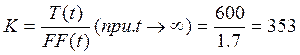 , где FF – соотношение расходов реагентов.
, где FF – соотношение расходов реагентов.
Постоянная времени реактора по каналу концентрации Т2 полностью определяется динамикой используемой системы измерения. Динамические же свойства непосредственно самого контура регулирования концентрации определяются, исходя из используемых технических средств. С учетом модернизации и интенсификации средств производства, общего улучшения динамических свойств применяемых САР динамические свойства данного контура регулирования можно в первом приближении принять равными динамике исполнительного механизма как наиболее инертного звена системы. Таким образом, учитывая тип используемого РО (регулирующий клапан 25Н32НЖ), принимаем постоянную времени канала концентраций, равную 25с.
Коэффициент усиления данного канала:
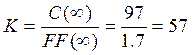
Время запаздывания по составу для реактора можно определить, используя время пребывания:
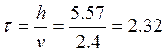 , где v – линейная скорость потока.
, где v – линейная скорость потока.
Передаточные функции имеют следующий вид:
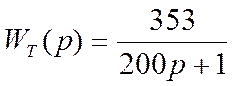
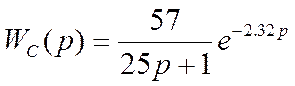
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.