3.СИНТЕЗ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ТЕХНОЛОГИЧЕСКИМ ПРОЦЕССОМ
3.1 Общие сведения
При автоматизации производственных процессов чаще всего задача синтеза сводится к выбору наиболее подходящего типового регулятора П, ПИ, ПИД - законами регулирования и определению его параметров настройки, обеспечивающих требуемый переходный процесс.
Выбор регулятора и определение его параметров настройки для объекта с известными характеристиками ведут в следующем порядке:
- исходя из особенностей технологического процесса, формируют требования к качеству регулирования, т.е. задаются некоторыми типовыми переходными процессами и его показателями;
- выбирают типовой закон регулирования;
- определяют параметры настройки регулятора;
- при вычисленных значениях настроечных параметров регулятора строят переходной процесс.
Структурная схема регулирования формирования первого слоя древесностружечного ковра при производстве ДСтП представлена на рисунке.3.1.
|
|
|
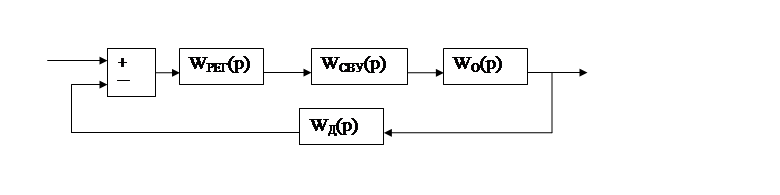
WРЕГ ─ передаточная функция регулятора; WСВУ ─ передаточная функция системы векторного управления; WО ─ передаточная функция объекта; WД ─ передаточная функция датчика.
Рис. 3.1
3.2 Получение линейной передаточной функции системы векторного управления
В результате нахождения общей передаточной функции системы векторного управления получаем высокий порядок, в этом случаи для редуцирования порядка воспользуемся следующей методикой.
На основании полученных результатов вычисления характеризующих систему векторного управления получены следующие графики переходных процессов.
На рисунке 3.2 изображен график изменения тока при номинальном режиме работы.
|
|
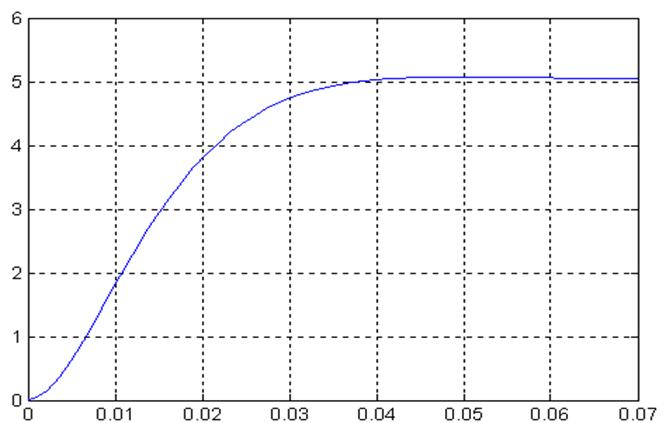
Рисунок 3.2
На рисунке 3.3 представлен график переходного процесса изменения скорости при номинальном режиме работы.
|
|
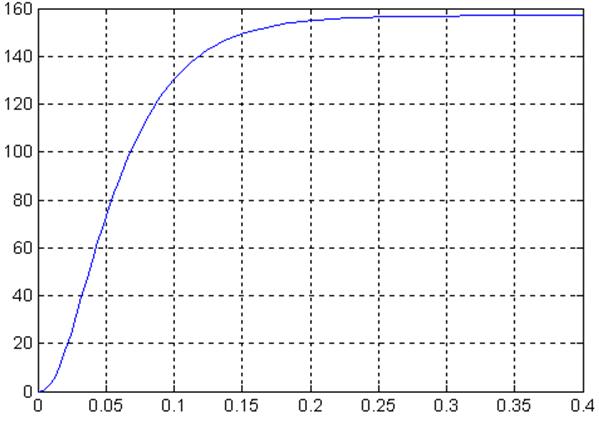
Рисунок 3.3
По графику переходного процесса изменения скорости, воспользуюсь методом площадей, определим передаточную функцию зависимости скорости от уровня.
Программа определения передаточной функции представлена в следующем виде:
clc;clear;clg;
dt=0.004;
h=[0 0.3433 2.1307 5.6613 10.7220 16.9544 23.9980 31.5404 39.3274 47.1617...
54.8937 62.4138 69.6445 76.5331 83.0471 89.1689 94.8924 100.2205...
105.1618 109.7300 113.9415 117.8151 121.3703 124.6273 127.6064 130.3275...
132.8097 135.0715 137.1303 139.0030 140.7047 142.2501 143.6528 144.9250...
146.0784 147.1235 148.0703 148.9276 149.7036 150.4057 151.0410 151.6155...
152.1350 152.6046 153.0292 153.4129 153.7596 154.0728 154.3558 154.6114...
154.8423 155.0508 155.2391 155.4091 155.5626 155.7012 155.8264 155.9394...
156.0413 156.1335 156.2166 156.2916 156.3593 156.4204 156.4756 156.5253...
156.5702 156.6108 156.6474 156.6805 156.7103 156.7372 156.7614 156.7833...
156.8031 156.8210 156.8371 156.8516 156.8647 156.8765 156.8872 156.8968...
156.9055 156.9134 156.9204 156.9268 156.9326 156.9378 156.9425 156.9467...
156.9505 156.9540 156.9571 156.9599 156.9624 156.9648 156.9668 156.9687...
156.9704 156.9718 156.9733]
h1=h/157;
n=length(h1);
i=1:n;
t=(i-1)*dt;
s1=dt*(sum(1-h1)-0.5*(1-h1(1)));
q=t/s1;
dq=q(2)-q(1)
s2=(s1^2)*dq*(sum((1-h1).*(1-q))-0.5*(1+(1-h1(n))));
y=step(157,[s2 s1 1],t);
plot(t,h,'ko',t,y)
grid
[s2,s1]
В результате выполнения программы получим
WСВУ=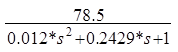
На рисунке 3.4 представлена сравнительная оценка полученного переходного процесса (изображено кружками) с первоначальным (сплошная линия) представлена на рисунке3.4.
График переходного процесса
|
|
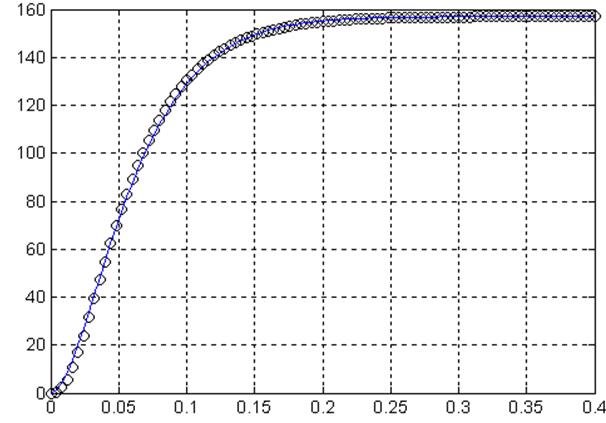
Рисунок 3.5
3.3. Произведем расчет ПИ регулятора.
Рассмотрим методику расчета ПИ-регулятора. Передаточную функцию регулятора представим в следующем виде:
![]() , (3.1)
, (3.1)
где Кп ─ коэффициент пропорциональности;
Ти ─ время изодрома.
Допустим, что у нас имеются два корня характеристического уравнения р1 и р2, которые находятся в непосредственной близости к мнимой оси координат. Эти корни и будут определять в основном всю динамику переходного процесса р1,2=α ± jβ. Имея пару доминирующих комплексных корней, привяжемся к показателю колебательности ψ:
![]() , (3.2)
, (3.2)
где m ─ степень затухания,m=α/β
Перейдем от р к jw и сместим мнимую ось на начало координат в точке желаемых корней, что дает переход W(p)ÕW(p-η),тогда получаем W(p) запишется в следующем виде:
![]()
![]() (3.3)
(3.3)
Выражение (3.3) является расширенной частотной характеристикой. В случаи нахождения корней на мнимой оси это будет говорить о том, что система находится на границе устойчивости.
Система находящееся на границе устойчивости записывается в следующем виде:
Wр((j-m)w*Wo(j-m)w =-1+jО (3.4)
Выделим мнимую и действительную часть Wр:
–С1-С0/((j-m)w)=mC0/((1+m2)w) – C1+jC0//((1+m2)w) (3.5)
![]() (3.6)
(3.6)
Ппреобразовав выражение (3.5) и (3.6), получаем:
mС0/((1+m2)w)-C1=Re(1/((Wo(j-m)w) (3.7)
С0/((1+m2)w)=Im(1/((Wo(j-m)w) (3.8)
Из выражений (3.7) и (3.8) находятся коэффициенты С1 иС2:
C1=Im(Wo((j-m)w)-1)*(1+m2)w (3.9)
C0=-Re((Wo((j-m)w)-1)-Im((Wo((j-m)w)-1)m (3.10)
Структурная схема системы регулирования имеет следующий вид, представленный на рисунке3.6:
Рисунок 3.6.
Расчет будем производить используя математический пакет Matlab.
Программа расчета коэффициентов настройки ПИ регулятора представлена в следующем виде:
clear,echo off
t1=0.005;
t2=0.4808;
t=1000;
h=0.0005;
m=0.85;
for v=1:t;
a=v*h;
W(v)=(0.1444*5)/((t1*a*(i-m)+1)*(t2*a*(i-m)+1));
C1(v)=imag(1/W(v))*a*(1+m^2);
C0(v)=-real(1/W(v))+(С1(v)*m)/(a*(+m^2));
end
plot(С0,С1’0’);
[k0,k1,button]=ginput(1)
В результате выполнения программы получаем следующие значение коэффициентов настройки регулятора:
С0 = 0,59
С1 = 2,36
Подставив значения С0 и С1 в структурную схему рисунок 3.6 получим следующий переходной процесс (рисунок 3.7)
|
График переходного процесса всей системы
|

Рисунок 3.7
3.4. анализ качества объекта регулирования
Качество объекта регулирования оценивают на основании полученного переходного процесса. Качество переходного процесса определяется по показателям [7], которые характеризуют отклонение реального процесса от желаемого.
Оценим показатели переходного процесса представленного на рис.4.3
1.t рег= 0,7.
2. удин= 0.035
3. уст= 0.001
4. Ψ== 0,02%
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.