Анализ технологического процесса как объекта управления. Система автоматизированного электропривода горизонтального конвейера

2.1. Анализ технологического процесса как объекта управления

Особенностью процессов протекающих в колонне К-102 является их большая сложность.

Эта сложность проявляется в значительном числе и многообразии параметров, определяющих течение процессов, в большом числе внутренних связей между параметрами, их взаимном влиянии друг на друга, причем изменение одного параметра вызывает нелинейные изменения других параметров. Отмеченная сложность в процессах, происходящих в атмосферной колонне, усиливается с наличием многих петель обратных связей между параметрами процесса, связанных со стриппинг-секциями и циркуляционными орошениями  (ЦО). Поэтому необходимо учитывать внутренние связи по всем каналам, для качественного регулирования системы.

Для применения общих принципов теории управления к управлению технологическим процессом необходимо его представить как объект управления.

Технологический процесс в атмосферной колонне можно представить в виде многомерного объекта (рис 2.1), на вход которого действует векторная переменная U(t) = [u₁(t),...,u_n (t)]  ,   а   выходные   переменные   процесса оцениваются вектором У(t) = [y₁ (t),..,y_m (t)] и возмущающие переменные процесса оцениваются вектором возмущения F(t)=[f₁(t)…f_i(t)].

Схема многомерного технологического процесса в колонне К-102 представлен на рис.2.1.

 

f₁(t)       .  .  .       f_i(t)

Колонна К-102

                         u₁(t)                                                         y₁(t)

                             .                                                                .

.                                                                .

u_n(t)                                                        y_m(t)

 

Рис.2.1. Схема многомерного технологического процесса в К-102.

u₁(t)…u_n(t)-входные параметры, n=1…5; y₁(t)…y_m(t)-выходные параметры, m=1…5; f₁(t)…f_i(t)-возмущения системы, i=1…3.

2.3. Разработка математической модели процесса

Математическая модель системы или процесса отражает в той или иной мере свойства реальной системы, в том числе ограничения, существующие в реальных условиях. Математическая модель составляется (разрабатывается) в математических терминах (на математическом языке) и имеет, как правило, количественное описание.

Каждая исследуемая система имеет m входных величин и n выходных величин. Между входными и выходными величинами существуют внутренние динамические связи, вид которых определяется соответствующими динамическими характеристиками.

Обозначим динамическую характеристику связи между i-м входом и j-м выходом передаточной функцией W_ij. Тогда динамическая система будет иметь mn характеристик. Они образуют характеристическую матрицу, описывающую все динамические свойства системы:

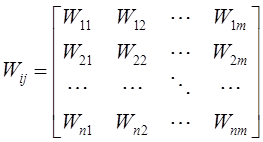                                                                               (2.1)

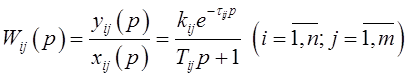                                                    (2.36)

где y_ij(p)–преобразованное по Лапласу значение выходной (регулируемой)                                                                    величины канала управления;

x_ij(p)–преобразованное по Лапласу значение входной (регулирующей, возмущающей) величины;

k_ij,_ij, T_ij,–соответственно коэффициент передачи, время запаздывания и   постоянная времени канала управления по i-ой входной и j-ой выходной переменным.

Согласно применяемому методу моментов зависимость (2.36) для любого канала может быть представлена  в следующем виде:

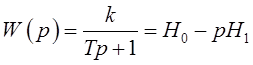                                                                               (2.37) где H₀, H₁–соответственно нулевой и первый моменты импульсной характеристики.

При этом момент H₀ соответствует коэффициенту передачи для данного канала управления, т.е.:

                                                                                                               (2.38)