Мякишев (10кл) стр.1-51(Физика, М. «Просвещение» 2004.)
« К » «Кинематика» изучает самое доступное для восприятия явление перемещения макротел в природе без учета причин вызывающих его. При этом ставится основная задача – определение положения тел в любой момент времени [Находим с помощью координатного способа - х(t), y(t), z(t), векторного способа - r(t) или естественного (траекторного) где задается положение точки на известной траектории в функции времени.] Эти способы взаимосвязаны и эквивалентны.
Для решения поставленной задачи потребовалось ввести :
3. Прямолинейное неравномерное движение – тело совершает за равные промежутки времени разные по модулю, но одинаковые по направлению перемещения.
4. Криволинейное равномерное – движение по дугам окружностей с постоянной по модулю скоростью.
5. Криволинейное неравномерное – движение по окружности с разной по модулю скоростью.
6.Относительность движения – тела двигаются по-разному относительно разных систем отсчета.
7. Система отсчета – это система координат связанная с телом отсчета и способ измерения времени.
8. Материальная точка – тело – точка, размерами которого можно пренебречь в данном случае.
9. Траектория – линия, по которой движется тело.
10. Абсолютно твердое тело – это система материальных точек, расстояния между которыми остаются неизменными во время движения.
11. Поступательное движение тел – любая прямая, проведенная в теле остается // самой себе.
12. Вращательное движение – все точки тела двигаются по окружности с центрами лежащими на одной прямой (оси вращения).
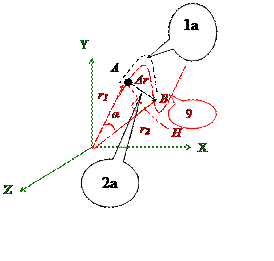
Δr2=AH2+HB2=r12sin2α+(r2-r1cosα)2=r12sin2α+r22-2r1r2cosα+r12cos2α=r12(sin2α+cos2α)-2r2r1cosα+r22=r12+r22-2r1r2cosα.
Теорема косинусов
[1а] ПутьL [м] - длина отрезка траектории (скаляр).
[2а] Перемещение - S [м] – вектор, связывающий начальное и конечное положения тела (точки А и В).
[ 3а] Скорость – физическая величина характеризующая быстроту изменения положения тел в пространстве.
[ 3б] Средняя путевая скорость - Vср = ∆ L /∆t [м/с] - ∆t - изменение времени. (весь путь делённый на всё время ,скаляр)
[ 3в] Мгновенная скорость – V = lim∆t→0 ∆S /∆t[м/с]. lim∆t→0 
, это предельное значение отношения 
при ∆t →0. (в данной
точке и в данный момент времени в этом случае ∆ L=∆S)
[ 4а ] Ускорение a [м/с2] - физическая величина которая характеризует направление и быстроту изменения скорости. (скорость изменения скорости)
[ 4б] Среднее ускорение aср = ∆V /∆t [м/с2].
[ 4в] Мгновенное ускорение a = lim∆t→0 ∆V /∆t [м/с2].
[ 4г] Центростремительное ускорение – ускорение тела при равномерном движении по окружности – обусловлено изменением направления скорости.
[ 5а ] Частота обращения n [об/с] - число оборотов в единицу времени.
[ 5б ] Период обращения T [с] - время одного оборота.
[5в ] Угловая скорость ω = ∆j / ∆t = V/R [рад/с] ∆j - приращение угла в радианах.
[ 6]
Среднеквадратическая скорость v = 
[
7] Изменение любой величины -разность
её конечного и начального значений.
Введенные понятия позволяют решить основную задачу кинематики для
простых движений , и .
G НО! На практике движение сложное и поэтому необходимо установить
II Положения, позволяющие решить основную задачу для сложного движения
1 Формула сложения скоростей – пусть имеется неподвижная система – Н, подвижная – n, а так же V
V – скорость
тела относительно Н, Vn – скорость тела
n Vn
относительно n и V0 – скорость n относительно Н, тогда
V = Vn + V0 умножая
на t => формула сложения Н
перемещений 
.Для ускорений а = аn. Для вектора R=Rn + R0
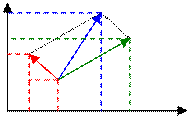2 Любой вектор (S, V или а) можно выразить через его проекцию на
координатные оси (разложить
на компоненты), Vy V = V1 + V2
при этом сумма проекций нескольких Vy1 V1 Vy = Vy1 + Vy2
векторов равна проекции суммарного Vy2 V2 Vx = Vx1 – Vx2
вектора. |V| = √ Vx2 + Vy2
. По проекциям вектора V Vx2 Vx Vx1
(Прх V = Vх ; ПруV = Vу) можно получить исходный вектор.
Установленные положения позволяют сложное движение разложить на простые его составляющие и результат получить как сумму. Поэтому целесообразно рассмотреть.
III Основные составляющие сложного механического движения
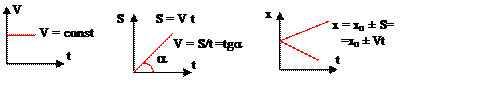1 Равномерное прямолинейное движение где x – координата, S – путь (площадь под V)
2 Равноускоренное прямолинейное движение
S=Vср·t; t = (V –V0) / a; S =((V0 + V) /2)·t =(V2 –V02) /2a.
аналогично по X, Y , Z
3 Вращательное движение jR – длина дуги j [рад]
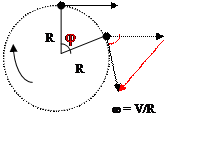A V1 |V1| = |V2| ; T =
1/ n [c] ; ω = ∆ j / ∆
t = 2 p /T = 2pn
R j B V = 2pR /T = 2pRn = ωR; если есть ∆V за ∆t, то
j j V1’ a = ∆V / ∆t Но! Если j → 0 AB / R ≈ ∆V / V Þ
ω ∆V =(AB /R)V Þ a = AB·V / R·∆t Но! Еслиj → 0
V2 ∆V AB ≈ ABÞ AB/ ∆t =VÞ a=V2 /R = ω2·R2/R = ω2·R = ω·V =
= 4p2 n2R=4p2 R/T2= центростремительное ускорение an [м/с2]
V1 =V2 =V
При j → 0 ∆V ^ V1 а = ∆V / ∆t Но !! ∆V = V1 ∆j = V1 ℓ / R; (∆j =sin j ; ℓ - длина дуги) Þ а =∆V / ∆t =Vℓ /∆t R = V2 / R; а ^ V1
Любое сложное движение, изучаемое в школе, можно разложить на вышерассмот- ренные , и , а затем, используя положение II получить решение, Но! анализ движения выше проведен без учета причин вызывающих его. Учет последних, производится в следующем разделе механики, где ответ на вопрос «Почему оно двигается?»
P.S. Для ссылок использовать при необходимости рубрикацию. Например, понятие «Угловая скорость» → < K. I. 5в >
Первые принципы кинематики
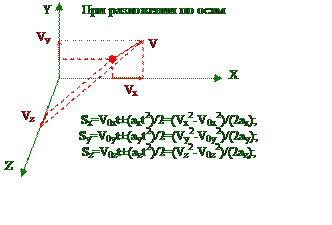
x(t)=x0+v0xt+axt2/2;
vx=v0x+axt;
y(t)=y0+v0yt+ayt2/2. vy=v0y+ayt.
«1 Кинематика» типовые задачи КЗ
1. Автомобиль двигается вдоль железной дороги прямолинейно равномерно с V = 60км./час. Когда он поравнялся с неподвижным локомотивом поезда, последний начал двигаться прямолинейно неравномерно с a = 2м / с2.Через какое время они встретятся (I.2; I.3; III.1; III.2)(I.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
