Моделирование систем массового обслуживания, описываемых случайным процессом «гибели и размножения»

процесса функционирования системы во времени, соблюдением таких же соотношений длительности операций как в системе оригинале. Имитируются элементарные явления, составляющие процесс, сохраняется их логическая структура, последовательность протекания во времени. В результате получается оценка характеристик системы.

1. Цель работы, задание

o  изучить методы аналитического и имитационного моделирования систем в приложении к решению конкретной задачи;

o  сравнить эффективность использования (простота, точность, объем вычислений) имитационных и аналитических методов для расчета показателей эффективности СМО.

Для достижения цели поставлены следующие задачи. Для системы массового обслуживания необходимо выполнить следующее:

1.  рассчитать вероятности состояний системы и характеристики эффективности СМО аналитически:

- определить тип системы массового обслуживания;

- построить размеченный граф состояний системы;

- выбрать расчетные формулы;

- рассчитать следующие показатели эффективности СМО:

·  вероятность загрузки системы;

·  вероятность отказа в обслуживании;

·  вероятность простоя системы;

·  вероятность нахождения в системе 1- ой заявки, 2 – х заявок, …, n – заявок;

·  среднее время обработки одной заявки;

·  среднее число занятых каналов;

·  среднее время ожидания в очереди;

·  среднее число требований в очереди;      

·  среднее число требований в системе;

·  среднее время нахождения заявки в системе.

2. Рассчитать вероятности состояний системы и характеристики эффективности СМО имитационным методом:

- составить блок-схему алгоритма имитации работы СМО;

- написать программу имитации с использованием любого языка программирования, любых программных средств;

- рассчитать программно показатели эффективности СМО, приведенные в п. 1.

3. Сопоставить результаты, полученные на основе использования аналитического и имитационного моделирования. Сделать выводы.

4. Оценить эффективность реализованной в контрольной работе системы массового обслуживания. Сформулировать предложения по улучшению работы СМО.

Вариант 8. В переговорном пунктеустановлено три телефона. Поток посетителей, приходящих на переговорный пункт, простейший пуассоновский с интенсивностью λ =0,2 (человек в минуту). Время разговора посетителей по телефону составляет в среднем: =10 минут (закон распределения интервалов между событиями показательный). Если все телефоны переговорного пункта заняты и в очереди 2 человека, то вновь пришедший посетитель покидает переговорный пункт. При имитационном моделировании задайте время работы переговорного пункта равным 800 часам (100 рабочим дням).

2. Исследование СМО аналитическими методами

Система является многоканальной с отказами и бесконечным потоком требований на входе – разомкнутая система.  

2.1.  Размеченный граф состояний

Пусть S₀, S₁,…, S_n – совокупность возможных состояний системы. Для любого фиксированного момента времени условные вероятности состояния системы в будущем зависят только от состояния системы в настоящем и не зависят от того, когда и откуда система перешла в это состояние. Предполагается ординарность суммарного потока всех событий в системе, т.е. одновременно не могут произойти два и более событий. Время перехода заявки из очереди на канал обслуживания и момент его освобождения предполагается нулевым. Число состояний в системе равно: N + m + 1, где

N = 3 – число каналов обслуживания

m = 2 – количество мест в накопителе очереди

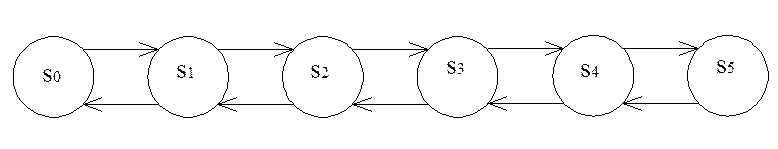S₀ – в системе нет ни одной заявки, простой

S₁ – в системе одна заявка, работает один телефон, два свободно

S2 – в системе две заявки, работают два телефона, один свободен

S3 – три заявки, все телефоны заняты

S4 – все телефоны заняты, в очереди один человек

S5 – все телефоны заняты, в очереди два человека  

2.2.  Определение вероятностей состояний

Из системы уравнений Колмогорова выводятся конечные формулы для расчета вероятностей состояний системы:

, , ,           

                            

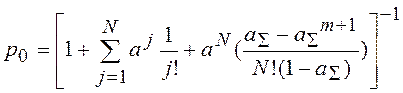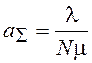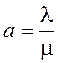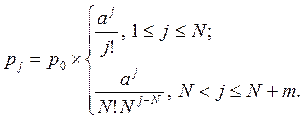
Интенсивность потока событий (среднее число событий, приходящееся на единицу времени – отношение единицы к среднему времени обслуживания)

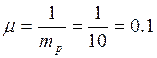
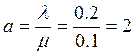
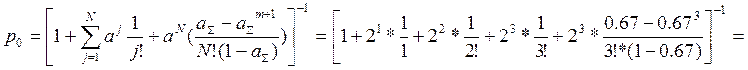= 1/7.80 = 0.128

P₁ = 0.2562

P₂ = 0.2562

P₃ = 0.1708

P₄ = 0.1139

P₅ = 0.0759

Вероятность загрузки системы:

 

Вероятность отказа в обслуживании, при :

         

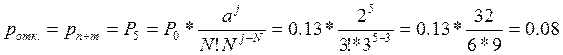
Относительная пропускная способность:

.             

Абсолютная пропускная способность:

.                    

Среднее число требований в очереди:

                               

Среднее время ожидания в очереди:

                 

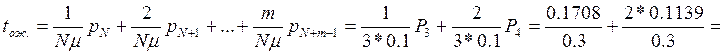
= 1.33

Среднее число занятых каналов:

0.2562+2*0.2562+3(0.1708+0.1139+0.0759)                           

= 1.85

Среднее число заявок в системе:

Среднее время пребывания требования в системе:

2.3.            Расчет основных показателей эффективности

3. Имитационное моделирование системы массового обслуживания

3.1.      Блок-схема алгоритма имитации

3.2.      Листинг программы имитации СМО

3.3.      Результаты работы программы имитации

QUEUE              MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME   AVE.(-0) RETRY

 QU                  2    2   5718      0     1.203     10.099     10.099   0

STORAGE            CAP. REM. MIN. MAX.  ENTRIES AVL.  AVE.C. UTIL. RETRY DELAY

 PHONE               3    1   0     2     5718   1    1.203  0.401    0    0

TABLE              MEAN    STD.DEV.       RANGE           RETRY FREQUENCY CUM.%

 TTIME             0.675    0.468                           0

                                      _  -       10.000          5716   100.00

 TORDER            0.675    0.468                           0

                                       _  -        0.000          1858    32.51

                                   0.000  -        2.000          3858   100.00

 PP0                      0          0.195                           

 PP1                      0          0.409                           

 PP2                      0          0.396                           

FEC XN   PRI         BDT      ASSEM  CURRENT  NEXT  PARAMETER    VALUE

 57474    0       48000.717   57474      5      6

 57489    0       48001.000   57489      0     15

 57487    0       48005.717   57487      0      1

 57481    0       48016.232   57481      5      6

 57490    0       96000.000   57490      0     13

Выводы

При анализе  систем массового обслуживания целесообразно работать с имитационными методами моделирования, поскольку это позволяет проводить эксперименты с несколькими наборами данных. Кроме того, использование имитационных методов моделирования  является менее