НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Моделирование»
ЛАБОРАТОРНАЯ РАБОТА № 5
МОДЕЛИРОВАНИЕ КРИЗИСНЫХ СИТУАЦИЙ В СИСТЕМАХ
МАССОВОГО ОБСЛУЖИВАНИЯ
Группа: АТ-23 Преподаватель: Студенты:Мартыко Н. Кухто А.В.
Переверзина Ю.
Новосибирск
2005
ЦЕЛЬ РАБОТЫ.
Получение практических навыков использования метода статистических испытаний Монте-Карло при моделировании кризисных ситуаций в системах массового обслуживания.
При моделировании такой системы решают 3 вопроса:
1. Среднее время нахождения объекта в очереди;
2. Среднее время ожидания объекта;
3. Закон распределения первых двух величин для заданных законов распределения интервала между приходом объектов и длительности обслуживания.
ЗАДАНИЕ 1.
Постройте имитационную модель для исследования работы пассажирского лифта в многоэтажном здании (N этажей). Все пассажиры едут с первого этажа и обслуживаются по очереди. Лифт вмещает одного человека. Время нахождения лифта в пути равняется N минутам, в зависимости от выбранного этажа. Используйте две случайные величины, распределенные равномерно: интервал между приходом людей к лифту (от 0 до Т минут) и время обслуживания (от 1 до N минут).
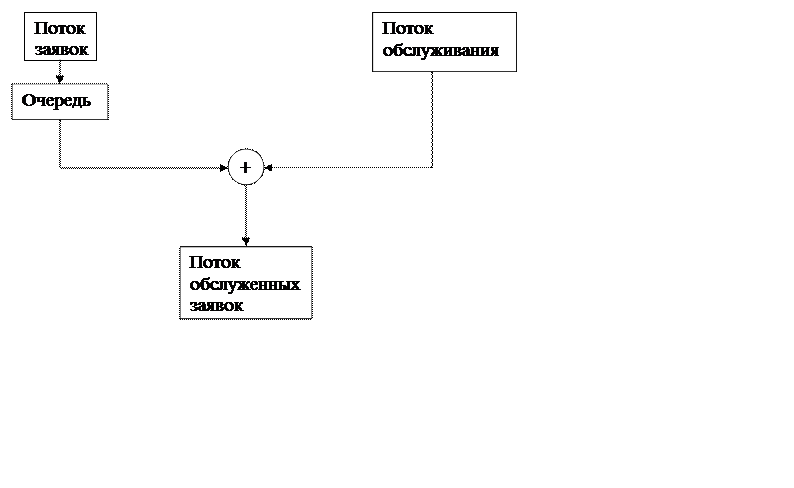
n – число человек (i=1…n).
Лифт один.
Ai – интервал между приходом пассажиров.
Bi – длительность обслуживания.
Ai и Bi генерируются и имеют заданный закон распределения.
Сi – время прихода пассажиров.
С1=0, Сi+1= Сi+ Ai+1.
Di – момент начала обслуживания.
Di+1=max(Сi+1+ Ei).
Ei – момент конца обслуживания.
Ei= Di+ Bi.
Fi – время, которое провёл пассажир в лифте и в ожидании лифта.
Fi= Ei - Ci
Gi – время нахождения в очереди.
G1=0, Gi= Fi-Bi .
Hi – время простоя лифта.
H1=0, Hi+1=Di+1-Ei .
Построим имитационную модель работы лифта с учётом вышеопределённых параметров.
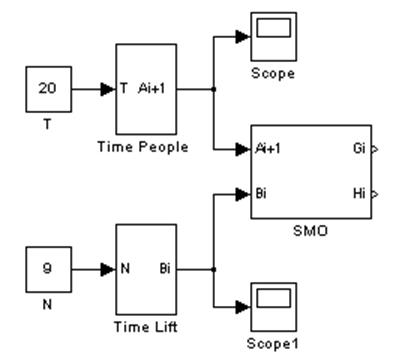
Рис. 1. Общий вид модели.
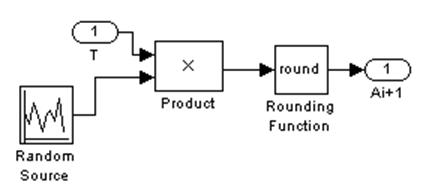
Рис. 2. Блок Time (временные интервалы между приходом людей к лифту и обслуживания).
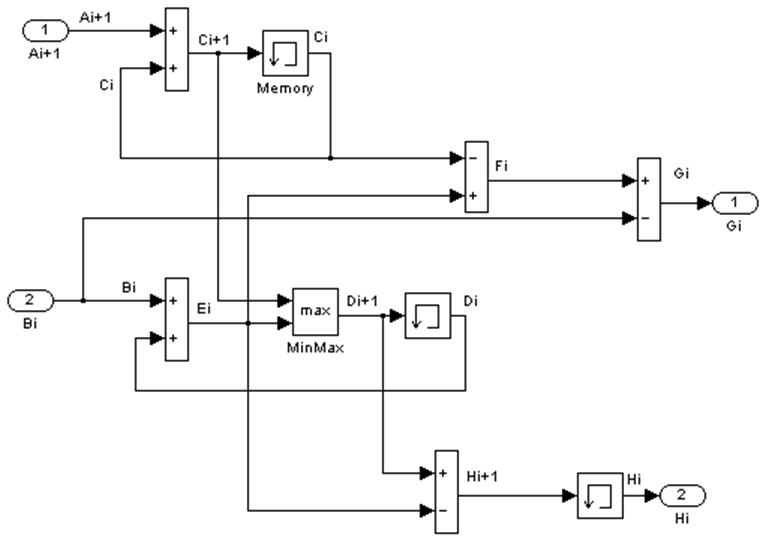
Рис. 3. Блок системы массового обслуживания.
На выходе этой системы получаем значения времени нахождения объекта в очереди и времени простоя лифта.
ЗАДАНИЕ 2.
Постройте гистограммы времени нахождения в очереди и времени простоя лифта. Оцените средние значения этих величин.
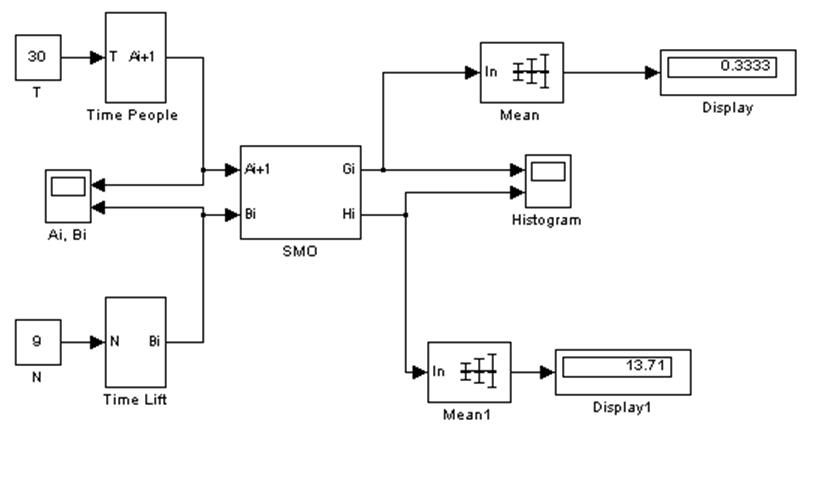
Рис. 4. Модель нахождения среднего и построения гистограммы.
В процессе моделирования получены следующие данные:
1. Распределенные равномерно: интервал между приходом людей к лифту (от 0 до Т минут) и время обслуживания (от 1 до N минут).
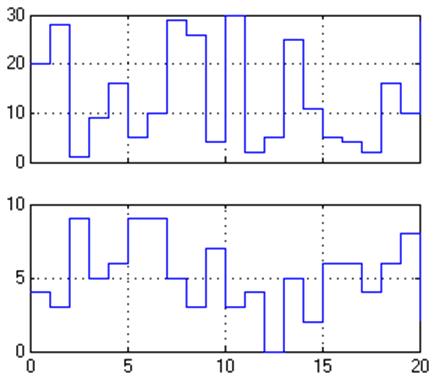
Рис. 5. Временные интервалы.
2. Гистограммы времени нахождения в очереди и времени простоя лифта.
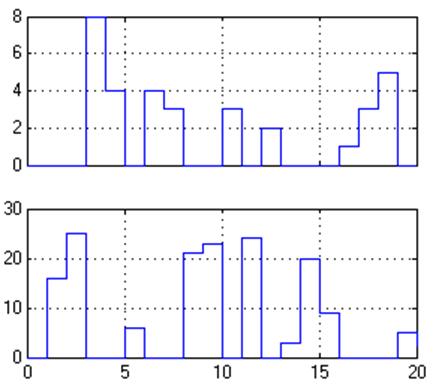
Рис. 6. Гистограммы времени нахождения в очереди и времени простоя лифта.
Среднее значение времени нахождения в очереди S1=1.571 мин.
Среднее значение простоя лифта S2=7.333 мин.
Данные были получены для интервала между приходом людей к лифту от 0 до 30 и времени обслуживания от 1 до 9 минут.
ЗАДАНИЕ 3.
Промоделируйте кризисную ситуацию, когда очередь к лифту неограниченно возрастает.
В нашем случае логично, что когда N→ ∞ и T→ 0, то возникает неограниченное возрастание очереди. Практически оно происходит, когда среднее время обслуживания больше среднего времени между приходом пассажиров.
Промоделируем кризисную ситуацию.
N=1…9, T=0…6.
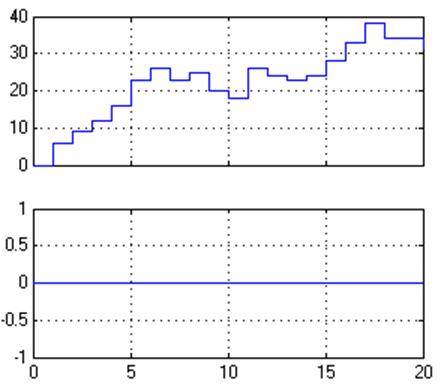
Рис. 7. Кризисная ситуация.
Из представленных гистограмм видно, что очередь возрастает, а время простоя лифта равно нулю.
ЗАДАНИЕ 4.
Повторите выполнение пунктов 2 и 3 для пуассоновского и нормального законов распределения случайных величин. Какое влияние оказывает закон распределения на результаты моделирования?
Среднее значение дисперсии у нормального закона больше, чем у пуассоновского, поэтому значения времени нахождения в очереди и времени простоя лифта изменяются довольно динамично для нормального закона.
В среднем результаты при распределении начальных значений по закону Пуассона были получены более удовлетворительные (при одинаковых параметрах модели).
N=1…9, T=0…30.
Нормальный закон: Gi=19.05, Hi=3.095.
Закон Пуассона: Gi=10.9, Hi=4.095.
ЗАДАНИЕ 5.
Измените модель таким образом, чтобы время обслуживания складывалось из суммы N минут на поездку к нужному этажу и M минут на возвращение лифта на первый этаж после поездки предыдущего пассажира.
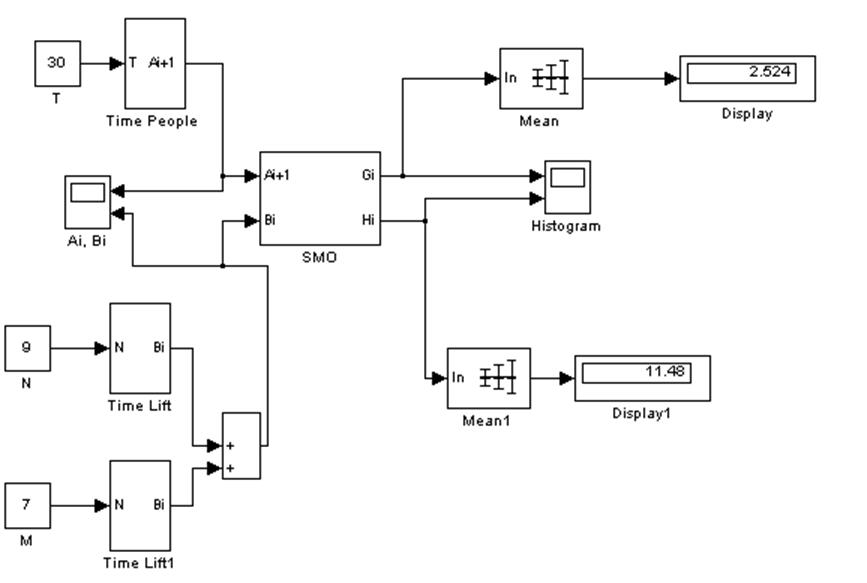
Рис. 8. Модель работы лифта с учётом времени его возвращения на 1й этаж.
В этом случае среднее время нахождения пассажиров в очереди увеличилось, так как увеличилось время обслуживания.
ЗАДАНИЕ 6.
Измените модель таким образом, чтобы она учитывала вероятность Р выхода лифта из строя при движении через каждый отдельный этаж.
В этом случае мы получаем неудовлетворительные результаты работы при значимой величине вероятности выхода из строя лифта.
Например, при параметрах системы, указанных в задании 2 и P=0.7, мы получили кризисную ситуацию (время нахождения в очереди бесконечно возрастает).
Если мы изменим значение вероятности P=0.01, то лифт работает в нормальном режиме
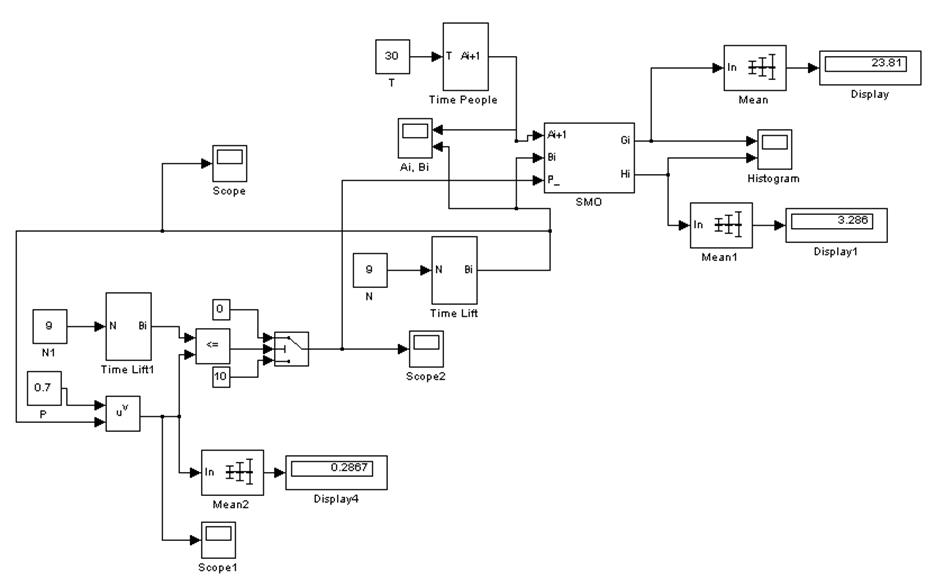
Рис. 9. Моделирование работы лифта с учётом возможности выхода его из строя.
ЗАДАНИЕ 7.
Добавьте в модель второй пассажирский лифт. Люди идут к тому лифту, очередь к которому меньше. Сравните работоспособность этого варианта лифта с исходным.
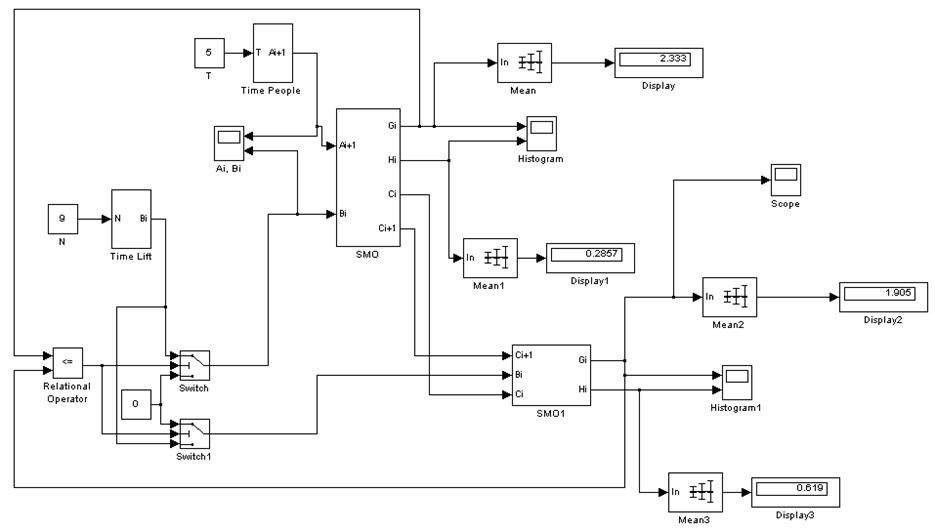
Рис. 9. Моделирование совместной работы двух лифтов.
Теперь нагрузка распределяется между двумя лифтами практически равномерно, так как пассажиры идут к лифту с меньшей очередью.
Вероятность возникновения кризисных ситуаций снизилась.
Например, при N=1…9 и T=0…5 кризисной ситуации не возникает.
То есть возникновение кризисов возникает при N>2*T.
ЗАДАНИЕ 8.
Добавьте в модель возможность пассажирам подниматься не на лифте, а по лестнице. Пассажиры начинают пользоваться лестницей, если длина очереди превышает S человек (очереди к лестнице не возникает).
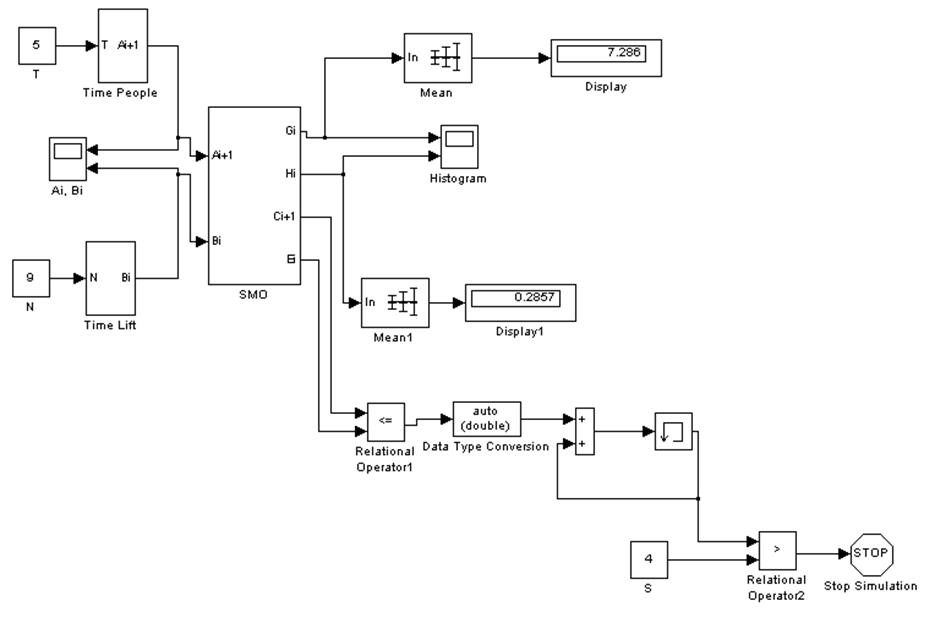
Рис. 10. Модель работы лифта при возможности использования лестницы.
N – число человек в очереди, то если пассажир пришёл до момента конца обслуживания предыдущего пассажира, то очередь увеличивается на единицу.
В случае использования лестницы мы можем регулировать длину очереди, то есть возможно избежать кризисных ситуаций, когда очередь неограниченно возрастает.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.