Проектирование и оптимизация схемы инвертора на n-МОП транзисторах, страница 2

По динамическим характеристикам  определяются параметры: время включения  и время выключения . Они определяются как моменты времени, в которые напряжения проходят уровни 0.1 или 0.9 логического перепада.

3. Моделирование статических характеристик инвертора

Существует достаточно большое число моделей статических характеристик МОП транзисторов, различных по точности и сложности. В данной работе для моделирования статических характеристик инвертора используется самая простая квадратичная модель, которая позволяет получить аналитические выражения статических характеристик и избежать необходимости решения нелинейных уравнений.

Эта модель представляет собой зависимость тока стока  МОП транзистора от его управляющих напряжений:

-   - напряжения “затвор - исток”;

-   - напряжения “сток - исток”;

-  - напряжения “подложка - исток”.

Она представляется следующими формулами:

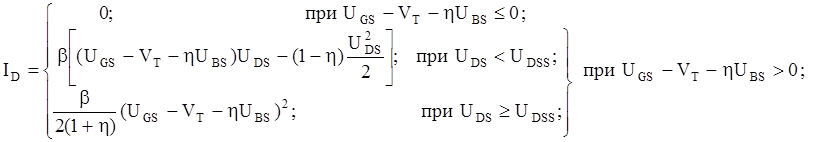                                                                                                                                        (1)

где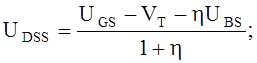      

Для n-канальных МОП транзисторов алгебраические величины  и  положительны, а  - отрицательна, но в выражение (1) все напряжения подставляются по модулю. Предполагаются их правильные полярности.

Параметрами модели (и МОП транзисторов) являются:

-   - пороговое напряжение, В;

-   - удельная крутизна, мА/В²;

-   - коэффициент влияния подложки.

Сразу отметим, что для инвертора параметры  и  транзисторов Т₁ и Т₂ одинаковы, т.к. они изготавливаются в одном технологическом процессе, но значения  и  различны. Последнее делается специально, для обеспечения хороших характеристик инвертора.

На характеристиках различают крутую область  и пологую . Напряжение  является граничным между этими областями.

Математической моделью инвертора является уравнение, сформированное по первому закону Кирхгофа для точки соединения транзисторов:

                                                                  (2)

с учетом показанного на рис. 1 положительного направления токов стока.

Подставляя в это уравнение выражения для токов по (1) с учетом для транзистора Т₁:

                                              (3)

для транзистора Т₂:

                     (4)

получаем уравнение, связывающее зависимость .

Транзистор Т₂ всегда находится в пологой области ВАХ, поэтому его ток представляется выражением:

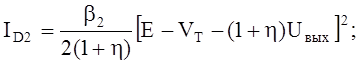                                                (5)

Когда , транзистор Т₁ закрыт и . Подстановка (5) в (2) позволяет получить, что  при этом равно:

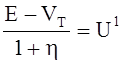;                                                                                              (6)

С учетом этого выражение для тока стока  в дальнейшем представляется как

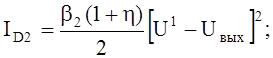                                                                 (5а)

При  транзистор Т₁ открывается. Сначала он находится в пологой области ВАХ. Подставка соответствующего выражения из (1) с учетом (3) приводит к зависимости:

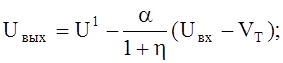                                                               (7)

где       .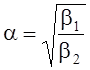

Ток инвертора на этом участке определяется затворным напряжением активного транзистора Т₁ и описывается квадратичной зависимостью:

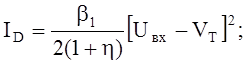                                                                                            (8)

В точке S (saturation) транзистор Т₁ заходит в крутую область ВАХ. Координаты этой точки получаются из выражения (7) (в ней оно еще работает) и уравнения

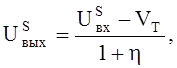
следующего из выражения  для транзистора Т₁ (см.(1)).

В результате получается

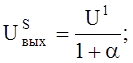
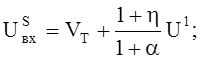                                                     (9)

Правее точки S  транзистор Т1 находится в крутой области ВАХ, уравнение передаточной характеристики (2) с учетом (1) и (5) представляет собой квадратное уравнение относительно :

                                                                             (10)

где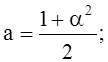                  

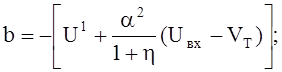                                                                (10a)

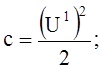
Его решение может быть легко найдено

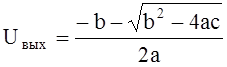;                                                                         (11)

Физический смысл имеет только знак (-) перед радикалом.

Выражение (11) позволяет рассчитать , которое получается при подстановке в (10а) .

Общий ток стока – ток потребления в состоянии логического нуля на выходе будет определяться выражением (5а):

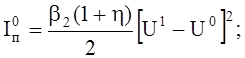                                                                       (12)

На рис. 5 и 6 представлены статические характеристики инвертора при различных значениях  при постоянном . Видно, что с уменьшением  характеристики становятся лучше, т.к. уменьшается напряжение логического нуля, растет логический перепад и увеличиваются запасы помехоустойчивости. Максимальный потребляемый ток уменьшается.