ряде задач вычислительной математики, связанных с моделированием физических процессов, приходится решать системы линейных алгебраических уравнений с трехдиагональной матрицей. В этом случае вместо методов Гаусса или LU-разложения более рационально использовать специальный метод - прогонки, который также изучается в данной работе.
Метод
Гаусса основан на замене исходной системы (1) на эквивалентную (т.е. имеющую
то же решение ![]() ), но с матрицей U верхней
треугольной формы:
), но с матрицей U верхней
треугольной формы:
![]() (2)
(2)
или в развернутом виде:
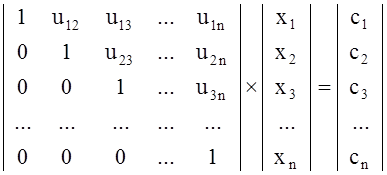 (2а)
(2а)
Матрица
U получается путем преобразования исходной матрицы A, а вектор ![]() - из вектора
- из вектора ![]() . Так
как матрица U - треугольная, все компоненты вектора
. Так
как матрица U - треугольная, все компоненты вектора ![]() ,
начиная с
,
начиная с ![]() , легко находятся последовательно.
, легко находятся последовательно.
Алгоритм метода Гаусса состоит из двух этапов:
Преобразование
A à U и ![]() . à
. à ![]() - прямой ход;
- прямой ход;
Последовательное
вычисление ![]() (i = n, n-1, ..., 1) – обратный ход.
(i = n, n-1, ..., 1) – обратный ход.
Далее приводится словесно-формульное описание алгоритмов прямого и обратного хода метода Гаусса. Обоснование проводимых операций можно найти в соответствующей литературе /1,2/.
Процедура
прямого хода осуществляется за n шагов (n - порядок СЛАУ). На k-том шаге
формируется k-тая строка матрицы U и k-тый компонент вектора ![]() .
.
Каждый
шаг состоит из двух частей. На первой вычисляются искомые элементы матрицы U и
компоненты вектора ![]() :
:
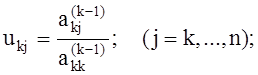
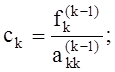 (3)
(3)
Примечание:
Индекс вверху (в скобках) означает индекс шага, от которого следует взять соответствующие
значения элементов и компонентов. Он необходим, так как на каждом шаге матрица
A и вектор ![]() преобразуются. Индекс k = 0
соответствует исходным элементам и компонентам. В дальнейшем будет видно, что
этот индекс является фиктивным, т.е. при программировании не порождает соответствующий
индекс массивов. Но при алгебраической записи формул в литературе он обычно
приводится.
преобразуются. Индекс k = 0
соответствует исходным элементам и компонентам. В дальнейшем будет видно, что
этот индекс является фиктивным, т.е. при программировании не порождает соответствующий
индекс массивов. Но при алгебраической записи формул в литературе он обычно
приводится.
На
второй части шага оставшаяся часть матрицы A (ниже k-той строки и правее k-того
столбца) и вектора ![]() (ниже k-того компонента)
пересчитываются по формулам:
(ниже k-того компонента)
пересчитываются по формулам:
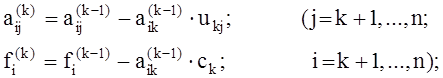 (4)
(4)
При k = n вторая часть шага не выполняется, т.к. пересчитывать больше нечего.
Обратный
ход начинается с определения ![]() , которое следует из
(2а):
, которое следует из
(2а):
![]() (5)
(5)
Затем
последовательно находятся ![]() по формуле:
по формуле:
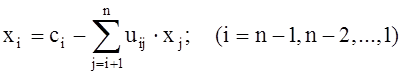 (6)
(6)
Эта
формула следует из обобщения уравнений, которые получаются при умножении
матрицы U на вектор ![]() из (2а) и рассмотрении их в
последовательности снизу вверх.
из (2а) и рассмотрении их в
последовательности снизу вверх.
Действия
с компонентами векторов ![]() и
и ![]() в (3) и (4) совпадают с аналогичными действиями
над элементами матриц A и U, поэтому в алгоритме Гаусса часто присоединяют эти
вектора в качестве дополнительного (n+1)-го столбца соответствующих матриц.
При этом алгоритм и реализующая его программа становятся более компактными и
красивыми.
в (3) и (4) совпадают с аналогичными действиями
над элементами матриц A и U, поэтому в алгоритме Гаусса часто присоединяют эти
вектора в качестве дополнительного (n+1)-го столбца соответствующих матриц.
При этом алгоритм и реализующая его программа становятся более компактными и
красивыми.
Метод LU-разложения основан на том, что матрица A может быть представлена в виде произведения двух матриц:
![]() (7)
(7)
где L - нижняя треугольная матрица,
U - верхняя треугольная матрица с единичной главной диагональю.
При этом разложении исходная система (1) разлагается на две, но с треугольными матрицами:
![]() (8а)
(8а)
![]() (8б)
(8б)
которые легко
решаются последовательно, т.е. сначала из решения системы (8a) находится
вектор промежуточных неизвестных ![]() , а затем, используя
найденный вектор
, а затем, используя
найденный вектор ![]() в качестве вектора свободных
членов, решается система (8b) и находится искомый вектор неизвестных
в качестве вектора свободных
членов, решается система (8b) и находится искомый вектор неизвестных ![]() .
.
Алгоритм разложения (факторизации) матрицы A на две треугольных также
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.