Алгоритмы и программы для работы с векторами и матрицами. Часть 2

работы алгоритма при возможных нулевых элементах в главной диагонали (в исходной матрице или полученных при пересчете) рекомендуется использовать процедуру выбора главного элемента. Она заключается в перестановке строк матрицы на каждом шагу ее приведения к треугольному виду перед осуществлением пересчета. Отыскивается строка, содержащая в k-том столбце наибольший по абсолютной величине элемент, а затем производится перестановка местами k-той строки и строки с этим наибольшим элементом. Только после этого осуществляется деление на . Каждая перестановка меняет знак определителя на противоположный. С учетом перестановок

где m - число перестановок строк при выборе главного элемента.

2.2. Вычисление обратной матрицы

Один из возможных методов вычисления обратной матрицы основан на решении матричного уравнения , где A - исходная, B- обратная и E - единичная матрицы:

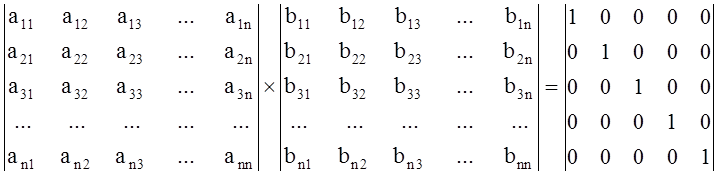
Это уравнение при умножении матрицы A на каждый столбец матрицы B распадается на n систем линейных алгебраических уравнений (СЛАУ):

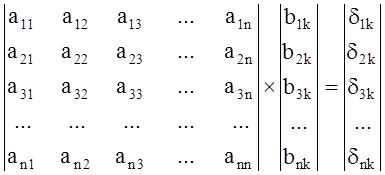,       где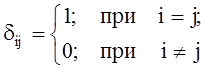     

(k = 1,2, …, n)

Решение каждой системы при k =1, 2 , ..., n позволяет определить k-тый столбец искомой обратной матрицы, т.е. процедура нахождения обратной матрицы сводится к n-кратному решению СЛАУ. Этот метод называется методом Жордана.

2.3. Вычисление матричных функций

После определения операции возведения квадратной матрицы в целую степень (см. предыдущую лабораторную работу) можно ввести понятие матричной функции матричного аргумента, используя представление функций в виде степенного ряда. Например, по аналогии с экспоненциальной функцией скалярного аргумента x

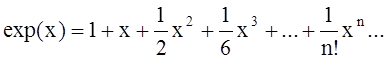
вводится экспоненциальная функция матричного аргумента X:

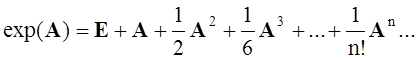
Аналогично можно представить sin(A), cos(A) и другие функции:

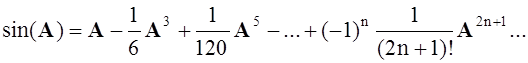
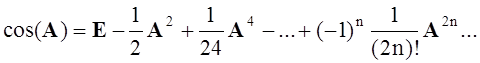
Суммирование членов ряда следует выполнять до тех пор, пока норма очередного слагаемого не станет меньше заданной погрешности e.

3. Готовые программы, используемые в работе

В работе рекомендуется использовать ряд готовых подпрограмм-функций, облегчающих работу с матрицами. Они объединяются в несколько модулей.

Подпрограммы модуля File99 (файл file99.cpp) предназначены для работы с файлами. Они позволяют записывать в файл на магнитном диске или считывать из него одномерные массивы – векторы и двумерные массивы – матрицы, а также согласованные совокупности двух или трех одномерных массивов. Для каждого из объектов имеется четыре подпрограммы-функции (две для записи и две для чтения), различающиеся списком параметров. В чем разница между ними, предлагается разобраться самостоятельно на основе анализа их текстов.

Для удобного ввода векторов и матриц рекомендуется использовать функцию IOVector из модуля Vector (файл vector.cpp) и функцию IOMatrix из модуля Matrix (файл matrix.cpp). Их использование требует подключение заголовочных файлов vector.h, matrix.h, define99.h и inter.h, а также объединение в проекте с головной программой и используемым модулем(лями) дополнительного модуля с сервисными функциями – inter.cpp. Кроме того, в заголовочном модуле define99.h необходимо заменить идентификаторы типов матриц и векторов с Vector на TVector  и Matrix на TMatrix.

Для вывода матрицы на дисплей можно использовать функцию DispMat в файле dispmat.cpp.

4.  Задание к работе

1)  Проанализировать тексты функций модуля file99. Разработать управляющие программы для функций WriteVec, ReadVec, WriteMat, ReadMat и опробовать их работу.

2)  Проанализировать тексты функций модулей Vector и Matrix. Разработать управляющие программы для функций IOVector и IOMatrix и опробовать их работу.

3)  Разработать подпрограмму-функцию для вычисления