Применение теоремы об изменении кинетической энергии к изучению движения механической системы: Методические указания к выполнению расчетно-графической работы по теоретической механике

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

НОВОСИБИРСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

МОСКОВСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА

ДИЗАЙНА И ТЕХНОЛОГИИ

(филиал)

"Применение теоремы об изменении кинетической энергии

к изучению движения механической системы"

методические указания

к выполнению расчетно-графической работы

по теоретической механике

для студентов направлений подготовки:

553900, 656100, 551800, 651600

специальностей:

280800 Технология швейных изделий

280900 Конструирование швейных изделий

281000 Технология кожи и меха

281100 Технология изделий из кожи

281200 Конструирование изделий из кожи

170700 Машины и аппараты текстильной и легкой промышленности

дневной формы обучения

Новосибирск 2008

Составитель:        д.т.н., профессор    А.М. Красюк

Рецензент:            к.т.н., доцент    В.П. Косых

Работа подготовлена кафедрой  МЕХАНИКИ

Методические указания к выполнению расчетно-графической работы по теоретической механике   "Применение теоремы об изменении кинетической энергии к изучению движения механической системы" -  Новосибирск, НТИ  МГУДТ (филиал),  2008,  8 с., Илл.5.

ВВЕДЕНИЕ

Данная работа посвящена решению задач динамики механической системы посредством теоремы об изменении кинетической энергии. Целью выполняемой расчетно-графической работы является развитие навыков составления дифференциальных уравнений движения механизмов и решение их с использованием вычислительной техники.

Работа состоит из двух этапов: подготовительного и этапа решения дифференциального уравнения на ЭВМ. В качестве исходных данных берется задание Д-10 «Применение теоремы об изменении кинетической энергии к изучению движения механической системы» в книге: А.А. Яблонский и др. Сборник заданий для курсовых работ по теоретической механики. – М., Высш. шк, 1985, 191-202 с. издание 4 и более поздние.

ПРИМЕНЕНИЕ ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ

ЭНЕРГИИ К ИЗУЧЕНИЮ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Механическая система под действием сил тяжести приходит в движение из состояния покоя, начальное положение системы показана на рисунке 1. Учитывая трение скольжения тела 1 и сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным S, а также построить графики зависимости пути пройденного первым телом, его скорости и ускорения от времени.

В задании приняты следующие обозначения:

т₁, т₂, т₃ – массы тел;

 - радиус инерции тела 2 относительно горизонтальной оси, проходящей через центр тяжести;

 - углы наклона плоскостей к горизонту;

 - коэффициент трения скольжения;

 - коэффициент трения качения.

Пример выполнения задания

Дано:

, , , , ,

; ;  ; ; ; .

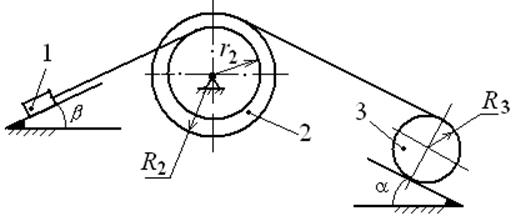
Рисунок 1

Решение:

Применим теорему об изменении кинетической энергии:

, где  - кинетическая энергия системы в конечном и начальном положении,

 - сумма работ активных сил на перемещении системы из начального положения в конечное. Т.к. в начальном положении система находится в покое, то . Определим кинетическую энергию системы по прошествию грузом 1 пути S. Она будет состоять из суммы энергий всех тел, входящих в систему.

.

Первое тело движется поступательно, следовательно

.

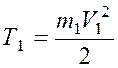Второе тело совершает вращательное движение, поэтому

.

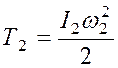 - момент инерции блока 2 относительно оси вращения.

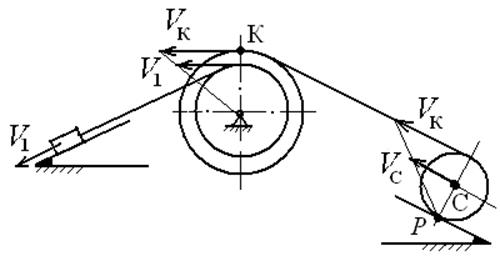
Рисунок 2.

Выразим угловую скорость 2-го тела,  через  (см. рисунок 2); 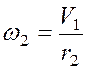, получим

.

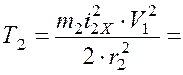
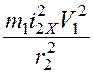Диск 3 движется плоскопараллельно, следовательно

.

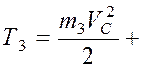
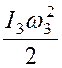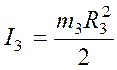 - момент инерции однородного диска, т.к. , то .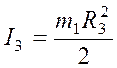

Выразим скорость центра масс 3-го тела  и  через скорость . Точка - мгновенный центр скоростей тела 3.

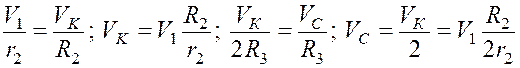            (1)

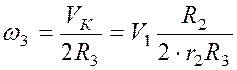,                                                                                 (2)

тогда получим

.

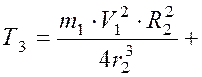
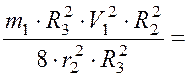
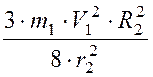Итак ,

,

.

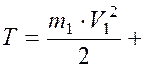
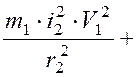
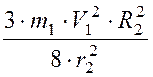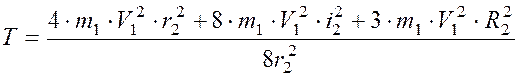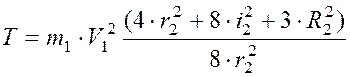Найдем сумму работ всех активных сил приложенных к системе на перемещении   S.

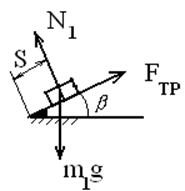Работа сил, действующих на первое тело будет состоять из работы силы тяжести и силы трения, рисунок 3.

Рисунок 3

На второе тело действуют силы тяжести, реакции опор и силы натяжения нитей (см. рисунок 4).  К активным силам относится только вес блока, однако работу он не совершает, так как опора неподвижная и перемещение ее равно нулю. .

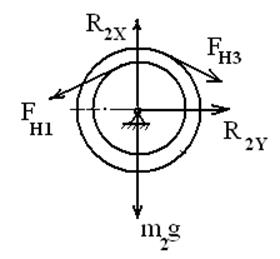Работа сил, действующих на третье тело, состоит из работы силы тяжести и работы момента сопротивления качению (см. рисунок 5).

,

где  - перемещение центра тяжести диска,  - угол поворота диска 3 при перемещении его центра навеличину .

Рисунок 4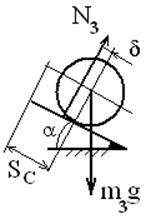

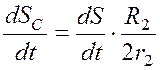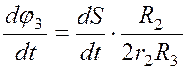Рисунок 5

Выразим  и  через перемещение первого тела. Запишем уравнение (1) и (2) в дифференциальной форме:

;              .

Очевидно, что

;                    .

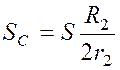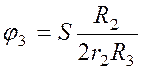Так, как , а , то

.

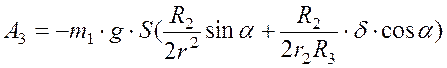Теперь запишем сумму работ всех активных сил действующих на систему .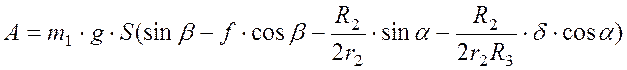

Согласно теореме об изменении кинетической энергии

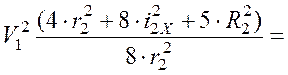
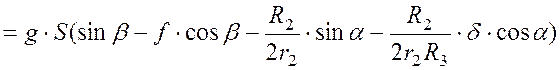
                                                 (3)

Откуда .

Для построения графиков зависимостей  воспользуемся методом Рунге-Кутта для численного решения дифференциального уравнения. В начале приведем уравнение (3) к виду: .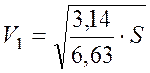

Запишем его в дифференциальной форме: .

Так как по условию задачи тело 1 двигалось из состояния покоя