Значения t-критерия Стьюдента при доверительной вероятности 0,90, 0,95 и 0,99, страница 2

4) Чтобы оценить уравнение линейной парной регрессии Y=a₀+a₁×X найдем значения параметров a₀ и a₁. Для этого в ячейку F18 введена формула =ОТРЕЗОК(C3:L3;C2:L2), а в ячейку F19 введена формула = НАКЛОН (C3:L3;C2:L2)

5) Для построения диаграммы рассеяния выделите диапазон ячеек А2:К3 и нажмите кнопку Мастер диаграмм  на панели инструментов. В диалоговом окне Мастер диаграмм (шаг 1 из 4):тип диаграммы задайте Тип графика Точечная, Вид Точечная диаграмма позволяет сравнить пары значений. Нажмите кнопку Далее. В следующем окне (шаг 2) нажмите кнопку Далее.

На шаге 3 на вкладке Заголовки задайте Название диаграммы Точечная диаграмма, Ось Х (категорий) Стоимость ТП, Ось Y (значений) Себестоимость ТП. На вкладке Легенда сбросьте флажок Добавить легенду. Нажмите кнопку Далее.

В последнем окне (шаг 4) нажмите кнопку Готово.

Чтобы добавить на диаграмму линию уравнения линейной регрессии, выделите маркеры на точечной диаграмме, а затем выполните команду меню Диаграмма→Добавить линию тренда… В окне Линия тренда на вкладке Тип укажите тип линии тренда Линейная. На вкладке Параметры установите флажки показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Нажмите кнопку ОК. На диаграмме добавится линии тренда, а также уравнение этой линии и коэффициент детерминации R² для данного варианта аппроксимации, характеризующий достоверность аппроксимации.

6) Спрогнозируем показатель Y (прогноз обозначим как ), если показатель X примет значение 125.

= a₀+a₁×125=86,706.

Для расчета прогноза  в ячейку F20 можно ввести формулу =F18+F19*125 либо формулу =ПРЕДСКАЗ(125;C3:L3;C2:L2) либо формулу =ТЕНДЕНЦИЯ(C3:L3;C2:L2;125;1), которая является более универсальной и часто используется при прогнозировании.

7) Доверительный интервал для прогноза Y находят по формуле

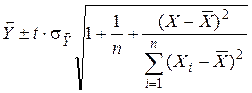, где t – коэффициент доверия, определяемый по распределению Стьюдента (рассчитан ранее в ячейке F17);

 – стандартная ошибка для оценки ;

 – средняя арифметическая показателя X.

.

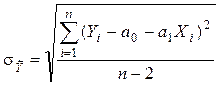Для расчета средней арифметической  в ячейке F21 использована формула =СРЗНАЧ(C2:L2)

Для расчета суммы квадратов отклонений от средней  в ячейке F22 использована формула =КВАДРОТКЛ(C2:L2)

Для вычисления множителя 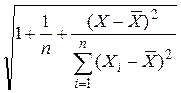 в ячейке F23 использована формула =КОРЕНЬ(1+1/10+(125-F21)^2/F22)

Для расчета среднеквадратического отклонения  в ячейку F24 введена формула =ИНДЕКС(ЛИНЕЙН(C3:L3;C2:L2;1;1);3;2)

Замечание. Статистическая функция ЛИНЕЙН возвращает параметры линейной аппроксимации данных. Функция ЛИНЕЙН возвращает параметры в виде массива значений. Искомое значение  расположено в третьей строке, во втором столбце. Для получения доступа к элементу массива использована функция ИНДЕКС.

В ячейку F25 введена формула =F20-F17*F24*F23

8) По аналогии с п.5 можно добавить другие линии тренда.

В списке доступных линий тренда Microsoft Excel отсутствует уравнение гиперболы. Для оценивания уравнения гиперболы введем преобразованный показатель Х’=1/Х в диапазон С27:L27. Чтобы добавить на диаграмму рассеяния точки, соответствующие уравнению гиперболы, щелкните правой кнопкой мыши по диаграмме и выберите в контекстном меню пункт Исходные данные… В окне Исходные данные щелкните по вкладке Ряд, затем нажмите кнопку Добавить. Для Ряд2 задайте следующие данные: Значения Х C2:L2 Значения Y C30:L30

9) Значения коэффициента детерминации R² для различных вариантов аппроксимации можно вывести на диаграмму рассеяния. Однако для уравнения гиперболы его необходимо рассчитать.

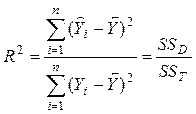, где  – средняя арифметическая показателя Y.

 – оценка уравнения регрессии в i-ой точке;

SS_D – обусловленная регрессией сумма квадратов;

SS_T – полная сумма квадратов.

В ячейку F31 введена формула =КВАДРОТКЛ(C30:L30)

В ячейку F32 введена формула =КВАДРОТКЛ(C3:L3)

Более удобным способом нахождения коэффициента детерминации R² является использование формулы

=ИНДЕКС(ЛИНЕЙН(C3:L3;C27:L27;1;1);3;1), которая не требует промежуточных вычислений SS_D и SS_T.

10) Показатель R² часто используется в качестве критерия для выбора наилучшего уравнения регрессии. Чем выше значение R², тем большую долю разброса относительно среднего  можно «объяснить» регрессией.

Приведем полученные значения R² для рассмотренных нами уравнений регрессии: линейная регрессия R²=0,7073; уравнение параболы R²=0,8185; степенная функция R²=0,6639, логарифмическая функция R²=0,6164; экспоненциальная функция R²=0,7479 и уравнение гиперболы R²=0,5111.

Отсюда можно сделать вывод, что наилучшим уравнением регрессии является либо парабола, либо экспонента. Однако визуально на диаграмме рассеяния более предпочтительно выглядят линейная регрессия и степенная функция.

К сожалению, в данном случае проявился известный недостаток показателя R² – он часто увеличивается с ростом числа параметров в уравнении регрессии, поэтому для параболы было получено наибольшее значение показателя R². Другая проблема, с которой мы столкнулись – это малый объем выборки. По 10 наблюдениям сложно делать однозначный вывод о наилучшем уравнении регрессии.

Для получения более обоснованных выводов о виде уравнения регрессии необходимо было бы провести дополнительные наблюдения. Также можно было бы использовать другие критерии выбора наилучшего уравнения регрессии (например, модифицированный R², критерий Маллоуса С_р и другие).