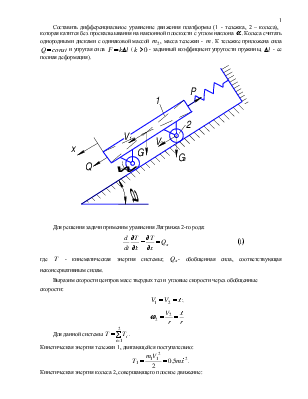

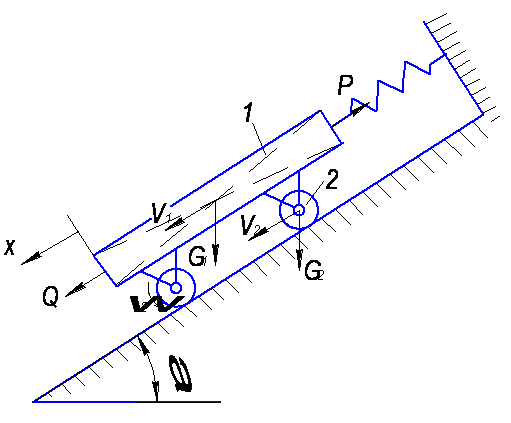
Составить дифференциальное уравнение
движения платформы (1 - тележка, 2 – колеса), которая катится без
проскальзывания на наклонной плоскости с углом наклона ![]() .
Колеса считать однородными дисками с одинаковой массой
.
Колеса считать однородными дисками с одинаковой массой ![]() ,
масса тележки -
,
масса тележки - ![]() . К тележке приложена сила
. К тележке приложена сила ![]() и упругая сила
и упругая сила ![]() (
(![]() -
заданный коэффициент упругости пружины,
-
заданный коэффициент упругости пружины, ![]() -
ее полная деформация).
-
ее полная деформация).
Для решения задачи применим уравнения Лагранжа 2-го рода:
![]()
![]()
где ![]() - кинематическая энергия системы;
- кинематическая энергия системы; ![]() - обобщенная сила, соответствующая
неконсервативным силам.
- обобщенная сила, соответствующая
неконсервативным силам.
Выразим скорости центров масс твердых тел и угловые скорости через обобщенные скорости:
![]() ;
;
![]()
Для данной системы 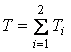 .
.
Кинетическая энергия тележки 1, двигающейся поступательно:
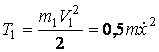 .
.
Кинетическая энергия колеса 2, совершающего плоское движение:
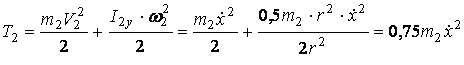 ,
,
где 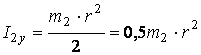 - момент инерции
тела 2.
- момент инерции
тела 2.
Тогда
![]()
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении.
Работа силы тяжести ![]() :
: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.