Характеристика одноканальных систем массового обслуживания с ожиданием. Решение задач линейного программирования транспортного типа распределительным методом

Время простоя оборудования может быть уменьшено путём увеличения численности обслуживающего персонала, а также созданием резервного парка оборудования, при котором суммарные производственные затраты (Э _произ) будут наименьшими.

Пусть λ-интенсивность потока требований на обслуживание, исходящих от единицы оборудования, и - среднее время обслуживания одного требования.

Обозначим через P_o вероятность того, что в данный момент на обслуживание не поступает ни одного требования и через P_k - вероятность нахождения в системе в данный момент k - требований из n - возможных (k=1,2,3,:,n).

Вероятности различных состояний системы определяют следующие соотношения:

,

,

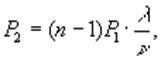
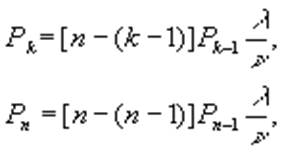(2)

Если величина P_о известна, то формулы (2) удобны для расчёта всех вероятностей.

Следующая вероятность P_k получается из предыдущей P_к-1 умножением на число [n -(k-1)] и на отношение

Для определения P_о выразим все P_k(k=1,2,3,:,n) чрез P_о и учтём, что сумма вероятностей всех возможных состояний системы равна единице. Получим:

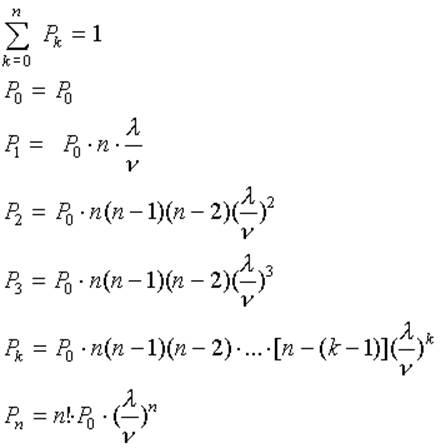
(3)

Суммируя левые и правые части этих равенств, получим:

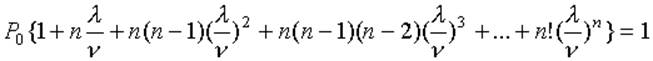(4)

Откуда и определяем P_о , а затем по уравнениям (2) все P_k

Зная P_k (k=1,2,3,:,n) можно вычислить основные числовые характеристики системы.

Обозначим через a - среднее число требований, находящихся в системе обслуживания:

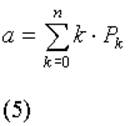
Разделив a на число устройств обслуживаемой совокупности, получим коэффициент простоя одного устройства (например, одного передатчика) в связи с пребыванием его в обслуживающей системе (обозначим его через a ):

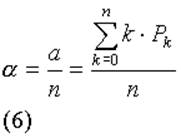
Вероятность того, что устройству придётся ждать своего обслуживания, равна (7)

Среднее число устройств, ожидающих обслуживания (обозначим его через b):

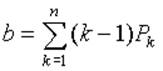(8)

Коэффициент простоя устройства в ожидании обслуживания b определяется соотношение средней длины очереди к числу обслуживаемых устройств:

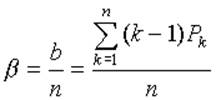(9)

Среднее время ожидания Т_ожид. Определяем умножением среднего числа устройств, ожидающих обслуживания, на средний промежуток времени между поступлением отдельных требований от обслуживающей системы: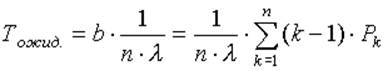 (10)

Коэффициент простоя обслуживающего персонала (человека) обозначается через

2.  Решение задач линейного программирования транспортного типа распределительным методом.

Распределительный метод является одним из наиболее простых способов решения транспортной задачи. Транспортные задачи сначала разрабатывались для определения наиболее экономичных планов транспортировки заданного вида продукции (ресурса) из нескольких пунктов - поставщиков ресурса (склады, заводы и т.д.) к нескольким потребителям ресурса (магазины, склады и т.д.).

Сущность транспортной задачи заключается в следующем:

заданы m источников ресурса и n пунктов его потребления. Запасы ресурса в источниках - A_i , i =1,¼ ,m; потребности - B_j , j =1,¼ ,n. Стоимость транспортировки единицы ресурса от i-го источника к j-му потребителю - C_ij; x_ij - количество ресурса, транспортируемого от i-го источника к j-му потребителю. Требуется определить такие значения x_ij , при которых общие транспортные расходы будут минимальны. Предполагается ресурсная сбалансированные задачи, то есть равенство общего запаса ресурсов у поставщиков и общего спроса на ресурс. Модель транспортной задачи, имеющую сбалансированные ресурсы, в литературе по экономико