где параметры с индексом «г» относятся к выхлопному газу (из сопел), «в» – к воздуху; n – коэффициент эжекции (считается заданным).

|
|

|
|
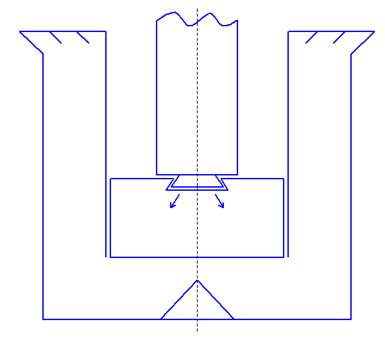
1. Уравнение количества движения (применительно к газовой динамике).
Для составлений уравнений газовой динамики выделяют замкнутый объем V, ограничивающий некоторую замкнутую поверхность.
Закон изменения количества движения:
изменение количества движения секундной массы газа ![]() в пределах
замкнутого объема V равен сумме всех
сил, приложенных к этому объему со стороны внешней среды:
в пределах
замкнутого объема V равен сумме всех
сил, приложенных к этому объему со стороны внешней среды:
![]() ,
,
где
![]() – массовый расход;
– массовый расход; ![]() – объемный расход (F – площадь живого
сечения, через которое движется газ со скоростью U),
– объемный расход (F – площадь живого
сечения, через которое движется газ со скоростью U), ![]() – вектор равнодействующих всех сил,
действующих на выделенный объем газа, со стороны внешней среды;
– вектор равнодействующих всех сил,
действующих на выделенный объем газа, со стороны внешней среды; ![]() и
и ![]() –
вектора скорости газа в начальном (откуда течет) и конечном сечениях потока.
–
вектора скорости газа в начальном (откуда течет) и конечном сечениях потока.
Закон количества движения записываем в виде проекции на оси выделенной системы координат, составляем уравнение проекции на Ох (вертикальная ось). Проекции сил, действующих в направлении, перпендикулярном оси Ох, равны нулю, т.к. поверхность ПС – цилиндрическая поверхность.
Отметим, что согласно первому свойству гидростатического давления: на внешней поверхности гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объема жидкости. Под внешней поверхностью жидкости понимают не только поверхности раздела жидкости с газообразной средой или твердыми стенками, но и поверхности элементарных объемов, мысленно выделяемых из общего объема жидкости.
Запишем уравнение изменения количества движения для рассматриваемой задачи:
![]() ,
,
где параметры с индексом «э» относятся к эжектируемому потоку, с индексом «д» – к параметрам на днище ракеты, без индекса – к искомым параметрам на нижнем срезе пускового стакана (нижняя граница замкнутого объема).
Распишем некоторые комплексы величин:
ρUF – массовый расход газа (кг/с);
![]() – количество движения секундной массы
газа;
– количество движения секундной массы
газа;
![]() – поверхностные силы давления,
действующие на рассматриваемую поверхность (по нормали внутрь выделенного
объема).
– поверхностные силы давления,
действующие на рассматриваемую поверхность (по нормали внутрь выделенного
объема).
Донное давление на днище ракеты ![]() будет отличаться от статического
давления в эжектируемом потоке, обтекающего ракету:
будет отличаться от статического
давления в эжектируемом потоке, обтекающего ракету:
![]() ,
,
где
![]() – коэффициент донного давления.
– коэффициент донного давления.
В
записанном выше уравнении количества движения неизвестными являются две
величины ![]() и
и ![]() , которые и можно из него выразить:
, которые и можно из него выразить:
![]() .
.
2. Уравнение расхода.
Суммарный расход в замкнутом объеме равен:
![]() или
или ![]() ,
,
где n – коэффициент эжекции (считается заданным).
Перепишем последнее выражение:
![]() или
или ![]() =
=![]() .
.
3. Уравнение энергии.
Необходимо определить температуру
торможения смеси выхлопного газа и воздуха в нижнем сечении пускового стакана ![]() . Температура торможения газа на срезе
сопла
. Температура торможения газа на срезе
сопла ![]() равна температуре торможения в камере
сгорания (а так как скорость газа в камере сгорания равна нулю, то температура
торможения в камере сгорания равна газодинамической температуре
равна температуре торможения в камере
сгорания (а так как скорость газа в камере сгорания равна нулю, то температура
торможения в камере сгорания равна газодинамической температуре ![]() ), т.е. она известная величина. На входе
в рассматриваемый объем имеем поток эжектируемого воздуха и поток выхлопного газа
из камеры сгорания, а на выходе – смесь выхлопного газа и воздуха (теплообменом
со стенками сооружения пренебрегаем, т.е. считаем процесс адиабатическим).
), т.е. она известная величина. На входе
в рассматриваемый объем имеем поток эжектируемого воздуха и поток выхлопного газа
из камеры сгорания, а на выходе – смесь выхлопного газа и воздуха (теплообменом
со стенками сооружения пренебрегаем, т.е. считаем процесс адиабатическим).
Запишем уравнение энергии:
![]() ;
;
![]() ;
;
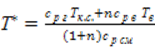 ;
;![]() ;
;
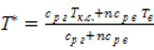 .
.
4. Уравнение состояния.
![]() .
.
5. Уравнение термодинамической температуры.
![]() .
.
Получена замкнутая система уравнений. Решение этой системы приводит к решению квадратного уравнения в нижнем сечении пускового стакана, следовательно, будем иметь два корня. Выбирается тот корень, который соответствует дозвуковому течению, т.к. в пусковом стакане отсутствует устройство, позволяющее создавать сверхзвук.
Определение параметров потока в выходном сечении пускового стакана
В данной задаче
требуется найти выходные параметры на срезе газохода вытекающего из него
потока: ![]() . Известными считаются параметры в
нижнем сечении пускового стакана, определенные в предыдущем пункте.
. Известными считаются параметры в
нижнем сечении пускового стакана, определенные в предыдущем пункте.
1. Уравнение баланса удельной механической энергии.
В выходном
сечении газохода течение является докритическим (дозвуковым). Конструирование
шахты требует выбора таких размеров выходного сечения газохода, при которых
истекающий поток через выходное сечение был бы докритическим. При дозвуковом
течении статическое давление в этом сечении газа должно быть равно наружному атмосферному
давлению. Если при дозвуковом течении появляется разность давлений между
статическим давлением в потоке и окружающим давлением, то она мгновенно ликвидируется,
так как вызванное этой разностью волны сжатия-разрежения, на которых происходит
выравнивание давления, могут распространяться как вверх, так и вниз по потоку. Таким
образом, ![]() .
.
|
|
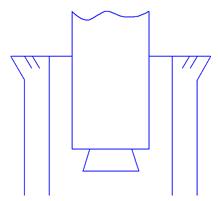
Запишем уравнение Бернулли для двух сечений: нижнего сечения на уровне нижнего среза пускового стакана и сечения на выходе из газохода:
![]() ,
,
где
![]() – суммарный коэффициент потерь,
учитывающий суммарные потери при повороте потока на 1800 на дне
установке и при выходе потока через газоотводящие решетки (считается
известным).
– суммарный коэффициент потерь,
учитывающий суммарные потери при повороте потока на 1800 на дне
установке и при выходе потока через газоотводящие решетки (считается
известным).
2. Уравнение расхода.
![]() ,
,
где n – коэффициент эжекции (считается заданным).
Выразим из последнего выражения искомые величины:
![]() .
.
3. Уравнение энергии.
Так как тракт теплоизолирован и отсутствуют потери энергии на нагрев стенок канала, то температура торможения сохраняется в потоке:
![]() .
.
4. Уравнение состояния.
![]() ,
,
где
![]() – удельная газовая постоянная смеси
выхлопного газа и воздуха.
– удельная газовая постоянная смеси
выхлопного газа и воздуха.
5. Уравнение термодинамической температуры.
![]() ,
,
где
![]() – удельная изобарная теплоемкость смеси
выхлопного газа и воздуха.
– удельная изобарная теплоемкость смеси
выхлопного газа и воздуха.
Получена
замкнутая система, позволяющая определить параметры в выходном сечении при
условии, что выбирается ![]() , соответствующее дозвуковому сечению.
, соответствующее дозвуковому сечению.
Оценка значений коэффициента эжекции
При решении данной задачи нет никаких условий для задания коэффициента эжекции. Мы должны оценить его истинное значение. Для этой оценки составляется уравнение баланса потерь удельной объемной механической энергии на местных сопротивлениях, т.е. должны использоваться коэффициенты местных сопротивлений (по справочнику).
Выбирается два основных коэффициента:
![]() – потери энергии при повороте на
1800 в нижней части установки;
– потери энергии при повороте на
1800 в нижней части установки;
![]() – потери энергии в верхней части
на газоотводящих решетках.
– потери энергии в верхней части
на газоотводящих решетках.
Уравнение баланса потерь.
![]() – в нижнем сечении
– в нижнем сечении
![]() – при выходе потока.
– при выходе потока.
Используя 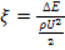 , запишем потери в рассматриваемых
элементах
, запишем потери в рассматриваемых
элементах
![]() ;
; ![]() .
.
Подставляем в уравнение баланса, получим
![]() .
.
Правая и левая часть уравнения определяется по условно заданному коэффициенту эжекции, который соответствует уравнению эжекции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.