Газодинамические схемы старта. Характеристика газодинамических процессов при старте ракет, страница 3

Исходными данными для определения параметров процесса являются геометрические размеры и параметры потока на выходе из сопла.

При входе эжектирующего потока в зазор нужно учитывать преобразование энергии (происходит потеря энергии вследствие образующихся циркуляционных зон при входе потока в зазор). Для этого необходимо знать безразмерный коэффициент местного сопротивления , который равен  (отношение потери удельной энергии  на местном сопротивлении к средней величине скоростного напора  в характерном сечении). Разновидностей местных сопротивлений, которые требуется учитывать, очень много.

U2

U1

Местное сопротивление

                                                            

Будем считать, что распределение параметров в сечении  и  является существенно неравномерным. Под механической энергией понимаем сумму кинетической и потенциальной энергий.

Рассмотрим случай, когда параметры потока в сечении распределены существенно неравномерно. Для неравномерно распределенных параметров выделим элементарные площадки dF с размером достаточно малым, чтобы в этих пределах пренебречь изменением параметров (по сечению площадки dF давление и скорость одинаковы).

dF

U

p

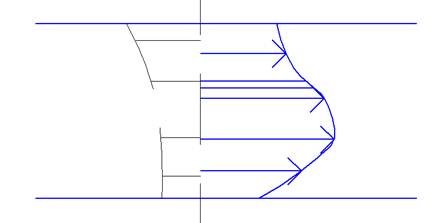
Рассмотрим движение газа через элементарную площадку dF. Введем некоторые понятия:

dV=UdF – секундный объем газа через площадку;

dm=UdF – секундная масса газа через площадку;

 – кинетическая энергия секундной массы газа;

pUdF – удельная потенциальная энергия секундной массы газа;

dF – механическая энергия секундной массы газа через dF.

Очевидно, что через всю площадь F в единицу времени проходит объем жидкости, определяемый следующем выражением: V=, при этом механическая энергия секундной массы газа определяется выражением: .

Удельная объемная механическая энергия (отнесенная к единице объема газа):

E=.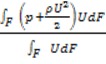

Для распределения параметров потока, который называется равномерным, выражение упрощается, т.е.

 .

В нашей задаче в покоящейся среде, откуда начинается движение газа, удельная объемная механическая энергия равна: , так как скорость газа равна нулю.

Введем понятие потери удельной механической энергии, равные

 .

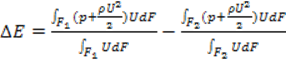Введем понятие коэффициента потерь  , выражаемого формулой:

 ,

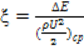где  – среднее значение скоростного напора в характеристики течения.

Это отношение обладает следующими свойствами (течение дозвуковое):

1.  не зависит от абсолютных размеров местного сопротивления, а зависит только от относительных размеров местного сопротивления (от геометрической формы).

d2 d

d1 d

D2 d

D1 d

U d

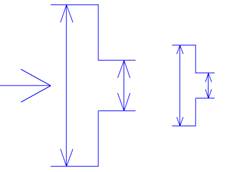
Если отношение диаметров одно и то же, т.е. , то   – одна и та же.

2. Не зависит  от параметров жидкости, протекающей через сопротивление, а также от свойств и рода жидкости.

Коэффициент зависит от того, где выбрать характерное сечение.

Местное сопротивление для определения исследуется экспериментально. При экспериментальном определении обязательно выбирается характерное сечение, и там замеряются значения скоростного напора. На основании результатов исследования местных сопротивлений составлены справочники, где указываются рекомендации по выбору характерного сечения.

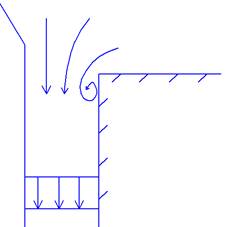
Определение параметров потока в зазоре между корпусом ракеты и стенками пускового стакана (эжектируемый поток – Iучасток)

Запишем следующие выражения для двух сечений: первое сечение – при входе потока в зазор (воздух считается неподвижным и давление равно атмосферному), второе сечение – сечение на уровне днища ракеты. Известны все геометрические размеры, а также параметры на срезе сопла. Индекс «э» – относится к параметрам эжектируемого потока, а индекс «г» – к параметрам выхлопного газа, истекающего из сопла, индекс «в» – к параметрам воздуха. В данной задаче требуется найти параметры эжектируемого воздуха в сечении на уровне днища ракеты (на рисунке днище не показано): .

pв ρв Tв Uв=0 d

pэ ρэ Uэ Tэ Tэ* d

1. Уравнение баланса удельной механической энергии.

Запишем уравнение Бернулли для двух сечений (воздух считаем несжимаемым):

,

где  – потери на местных сопротивлениях – вихреобразование при входе потока в канал, образующимся при внезапном сужении потока ( считается известным).

Сгруппируем слагаемые и получим:

.

2. Уравнение расхода.

Коэффициент эжекции считаем заданным: , где  секундный расход газа через сопло,  – секундный расход эжектируемого воздуха.

Откуда и

.

3. Уравнение энергии.

Запишем выражение для полной удельной (Дж/кг) энергии (полной удельной энтальпии) в общем виде:

H=,

где  = – удельная энтальпия;  – удельная внутренняя энергия;  – удельная потенциальная энергия;  – удельная кинетическая энергия;  – удельная изохорная теплоемкость газа (Дж/кг/К);  – удельная изобарная теплоемкость газа.

Запишем уравнение энергии для двух рассматриваемых сечений:

  (скорость воздуха равна нулю U_в=0), сократим на  и получим

.

Заметим, что  , где – температура торможения эжектируемого потока, т.е. та температура газа, которая получится, если затормозить движущийся газ адиабатическим путем (без подвода или отвода тепла).

С учетом последнего выражения предпоследнее выражение можно переписать в виде (тракт теплоизолирован, т.е. нет теплообмена со стенками сооружения):

.

4. Уравнение состояния идеального газа.

,

где  – удельная газовая постоянная воздуха (Дж/кг/К).

Вследствие того, что коэффициент эжекции n считаем заданным, полученная система уравнений – замкнутая.

Параметры потока в нижнем сечении (IIучасток)

К числу известных величин относят параметры эжектируемого потока в зазоре между корпусом ракеты и стенками пускового стакана (ПС), а также параметры потока в выходном сечении сопла. Все геометрические размеры заданы. В данной задаче требуется найти параметры смеси выхлопного газа, истекающего из сопла, с воздухом в нижнем сечении пускового стакана: .

При верхних положениях ракеты в выходном сечении ПС параметры смеси воздуха с выхлопным газом во всех точках одинаковы. Для составления уравнений необходимо выделить объем и применить к этому объему основные уравнения газовой динамики.

Параметры смеси газов:

,