Графический метод определения интенсивности инерционного сдвигового течения сыпучей среды в горизонтальном вращающемся цилиндре

УДК 624.131 + 631.362

В.А. Патрин к.т.н., А.В. Патрин инженер

ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ ИНЕРЦИОННОГО СДВИГОВОГО ТЕЧЕНИЯ СЫПУЧЕЙ СРЕДЫ В ГОРИЗОНТАЛЬНОМ ВРАЩАЮЩЕМСЯ ЦИЛИНДРЕ

Новосибирск, НГАУ

Водопадный режим движения в горизонтальном вращающемся цилиндре представляет сложную систему механического движения сыпучей среды включающую:

а) Вращательное движение, обеспечивающее переход сыпучего тела на более высокий потенциальный энергетический уровень;

б) свободный полёт частиц, когда сыпучая среда как система перестаёт существовать. Потенциальная энергия переходит в кинетическую энергию полёта частиц;

в) инерционное сдвиговое течение частиц в момент образования сыпучего тела.

В настоящей работе поставлена задача количественной оценки сдвигового течения сыпучей среды в момент её падения (рис. 1).

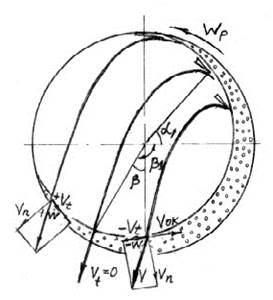
Рис. 1 Движение зерна с отрывом лопатками в цилиндрическом решете.

Величина сдвигового течения определится разницей соотношений кинематических уровней энергии двух соприкасающихся потоков зерна – падающего и движущегося вместе с поверхностью цилиндра:

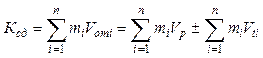                                          (1)

где:      - масса зерна отрываемая i – той лопаткой;

 - относительная тангенциальная скорость падающего слоя зерна от i – той лопатки;

 - касательная составляющая скорости падения слоя зерна от i – той лопатки;

V_ок ≈  - скорость зерна движущегося вместе с поверхностью цилиндра.

Знак минус принимается при совпадении направления потоков и плюс при наличии противотока.

В предыдущей работе [2], были получены уравнения, по которым определяются необходимые параметры в точках падения зернового потока при различных кинематических режимах цилиндра и углах отрыва зерна.

Предполагаем, что относительная касательная скорость  стремится к нулю, а количество движения  полностью расходуется на сдвиговое течение сыпучей среды.

Так как величина изменения радиуса установки первой и последней лопатки составляет не более 3 % по отношению к радиусу цилиндра, то считаем r = const.

Перейдём к теореме Эйлера об изменении количества движения сплошной среды [1].

В любой момент суммарное количество движения, которое имеет падающий поток в касательном направлении к окружности определиться выражением:

                                                               (2)

Момент количества движения относительно центра цилиндра.

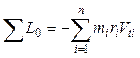                                                                         (3)

Дальнейшее решение задачи выполняем в плоскости в безразмерных параметрах, приняв:

;           ;           .

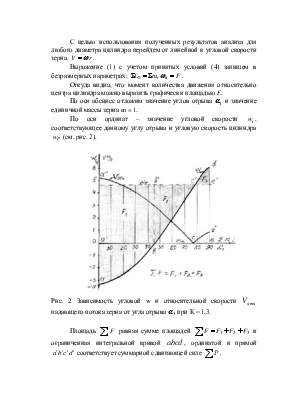
С целью использования полученных результатов анализа для любого диаметра цилиндра перейдем от линейной к угловой скорости зерна. .

Выражение (1) с учетом принятых условий (4) запишем в безразмерных параметрах: .

Откуда видно, что момент количества движения относительно центра цилиндра можно выразить графически площадью F.

По оси абсцисс отложим значение углов отрыва  и значение единичной массы зерна m = 1.

По оси ординат – значение угловой скорости , соответствующее данному углу отрыва и угловую скорость цилиндра  (см. рис. 2).

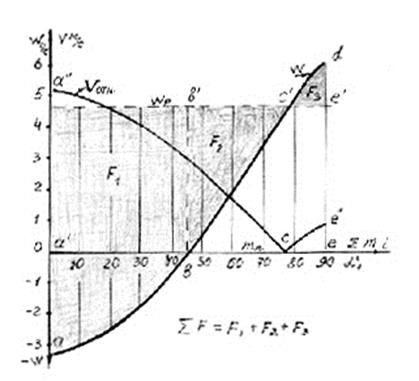
Рис. 2 Зависимость угловой w и относительной скорости  падающего потока зерна от угла отрыва  при К = 1,3.

Площадь  равная сумме площадей  и ограниченная интегральной кривой , ординатой и прямой  соответствует суммарной сдвигающей силе .

При отрыве зерна лопатками, установленными под углом , имеет место противоток. Относительная величина угловой скорости равна сумме ординат . Величина сдвигающей силы на данном участке соответствует площади .

При углах отрыва от  до  угловая скорость падающего потока совпадает с направлением вращения цилиндра,, при этом относительная угловая скорость уменьшается до нуля в точке С. В точке “C” угловая скорость падающего потока совпадает по величине и направлению с угловой скоростью цилиндра.

Величина сдвигающей силы на данном участке определяется площадью .

При углах отрыва  угловая скорость падающего потока больше угловой скорости цилиндра, а относительная величина угловой скорости равна разности отрезков .

Сдвигающий момент количества движения на данном участке определится площадью .

Абсолютная величина сдвигающего момента количества движения определится

где  - масштаб угловой скорости и массы.

На рис. 1 кривая  характеризует изменение относительной скорости  при встрече двух зерновых потоков – падающего и движущегося вместе с поверхностью цилиндра.

Относительная скорость построена в зависимости от угла отрыва  при кинематическом режиме К = 1,3, радиус решета R = 0,6 м и изменяется от 5,06 м/с при угле отрыва  до нуля при , затем увеличивается до 1 м/с при угле отрыва  и опережает скорость решета.

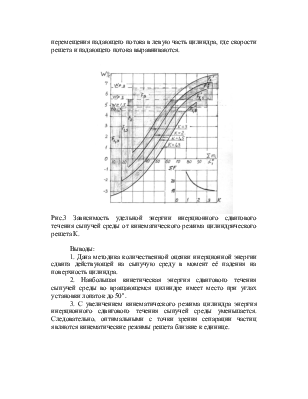
На рисунке 3 построены интегральные кривые и площади, определяющие энергию сдвигового течения сыпучей среды для кинематических режимов К = 1,3; 1,5; 2; 3 цилиндрического решета r = 0,6 м.

Из графика видно, что с увеличением кинематического режима решета при одинаковой загрузке и углах установки лопаток интенсивность сдвигового течения сыпучей среды уменьшится за счёт перемещения падающего потока в левую часть цилиндра, где скорости решета и падающего потока выравниваются.

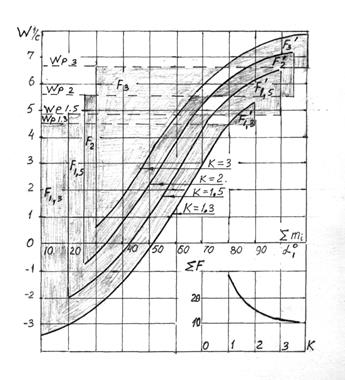
Рис.3 Зависимость удельной энергии инерционного сдвигового течения сыпучей среды от кинематического режима цилиндрического решета К.

Выводы:

1. Дана методика количественной оценки инерционной энергии сдвига действующей на сыпучую среду в момент её падения на поверхность цилиндра.

2. Наибольшая кинетическая энергия сдвигового течения сыпучей среды во вращающемся цилиндре имеет место при углах установки лопаток до 50°.

3. С увеличением кинематического режима цилиндра энергия инерционного сдвигового течения сыпучей среды уменьшается. Следовательно, оптимальными с точки зрения сепарации частиц являются кинематические режимы решета близкие к единице.

Литература:

1.  Беляев      . Теоретическая механика.

2.  Патрин В.А., Патрин А.В. Принудительный отрыв и свободное падение сыпучей среды в горизонтальном вращающемся цилиндре. В печати.