Непосредственное измерение физических величин. Первичные величины. Косвенное измерение физических величин. Вторичные величины, страница 3

Во-первых, вторичные величины, как и первичные, должны отвечать Принципу абсолютности отношений. Во-вторых, должно быть обеспечено строгое соответствие между относительным изменением численных значений вторичной и первичных величин. В-третьих, размерность вторичной величины (при метрических преобразованиях первичных величин) должна быть равно размерности правой части. Последнее требование будет рассмотрено позднее. Если для первичных величин Принцип выполняется автоматически, то для вторичных он может выполняться при определенных условиях: численные значения вторичных величин (7.5а и 7.5б), полученные в результате метрических преобразований первичных, должны быть пропорциональными.

Данное условие выполняется, если метрические преобразования правой части выражения (7.5а) приводят к пропорциональному изменению его левой части. С этой проблемой мы уже сталкивались. В разделе 2.3 было показано, что степенные комплексы вида (2.15) обладают свойством абсолютной однородности: пропорциональное изменение аргументов комплекса приводит к пропорциональному изменению самого комплекса. При этом коэффициент преобразования комплекса «y_c» равен степенному комплексу, состаленному из множителей преобразования

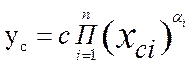
Как физические так и метрические преобразования – суть подобные преобразования, поэтому выражение (2.16а) напишем применительно к выражению (6.5б)

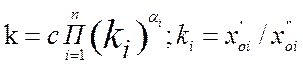
Итак, условие (7.6) выполняется, если уравнение (7.4) представляет собой однородную функцию

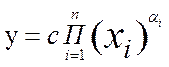                                                        (7.8)

где x_i – первичные величины, которые входят в определительное уравнение; - показатели степени легко устанавливаемых в конкретных задачах; с – некоторых коэффициент пропорциональности. Внося в данное выражение численные значения вторичных величин, получим

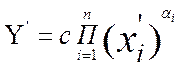                                                    (7.9а)

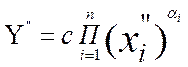                                                   (7.9б)

Далее, подставим в последнее выражение Х^” из (7.2а)

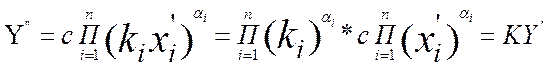
Полученное соотношение отвечает условию (7.6) и, следовательно, отвечает Принципу абсолютности отношений. Коэффициент метрических преобразований K равен

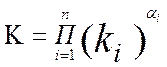                                                      (7.10)

Функция (7.10) – функция однозначная, множитель преобразования K обеспечивает строгое соответствие между относительным изменением численных значений вторичной и первичных величин. В качестве примера неоднозначной функции можно указать функцию . Предоставляем убедиться в этом самому читателю.

7.3 Размерности физических величин. Формула размерности.

1. В 1822 году Ж. Фурье в своей работе «Аналитическая теория теплоты» ввел два понятия, которые в современной трактовке можно рассматривать как понятие о размерности физических величин и понятие об одноразмерности физических уравнений.

2. Желая сказать, что длина измеряется в метрах, время в секундах мы говорим, что размерность длины является метр, размерностью времени – секунда. При этом операция сложения (вычитания) возможно только в том случае, если слагаемые, величины одноразмерны. Так, можно говорить о сумме 5м + 10м; 8кг + 2кг; 10Н + 2Н. Выражение 5м + 4Н; 2кг + 1.5с лишено всякого физического смысла.

Как уже говорилось, сопряжение вторичной величины с числом происходит на основе математических действий. Например, если точка движется равномерно и проходит расстояние 5м за 2с, то ее скорость равна V = 5м/2с = 2.5м/с. Мы видим, наряду с действиями над цифрами, мы выполняем математические операции над размерностями.

Используя понятия об одноразмерности физических уравнений и размерности физической величины, сформулируем требования, которым должны отвечать физические формулы, уравнения и т.п. (правило Фурье).

3. Сложение (вычитание) двух и более величин возможно только в том случае, если размерности величин одинаковые.

4. В математических выражениях, формулах и т.п., связывающих те или иные физические величины, левые и правые части означенных соотношений должны быть одноразмерными.

5. В настоящее время размерность величины определяется следующим образом. Если с изменением величины «x» в «k» раз численное значение величины «y» увеличивается в раз, то говорят, что величина «у» имеет размерность по отношению к величине «x».