Независимость отношения численных значений одноименных величин есть характерная и важная особенность рассмотренных нами величин, которая получила название Принципа абсолютности отношений. Означенный Принцип можно выразить в виде соотношения:
X”’I / X”i = X”I / X’I = ki, (i=1,2,…,n)
где X”’i, X”i, X’I, X – численные значения величины х, соответствующие её ЕИ х0i”’, х0i”, х0i’
Подведем итог. Нами рассмотрены величины обладающие следующими особенностями: а) сопрягаются с числом путем непосредственного измерения; б) ЕИ означенных величин выбираются произвольно по отношению к другим величинам; в) Принцип абсолютности отношений выполняется автоматически.
Величины, имеющие указанные особенности, получили название первичных.
7.2 Косвенное измерение физических величин. Вторичные величины.
1. Процесс измерения физических величин, изложенный выше, можно распространить, в принципе, на все известные нас величины. Возможно так и было в древности, когда люди непосредственно измеряли те или иные величины. С развитием производства, экономики, науки появлялось все больше величин, которые нужно было измерять. В какой-то момент времени было замечено, что численные значения некоторых величин можно вычислять, предварительно измерив величины, от которых зависела измеряемая величина. Например площадь прямоугольника А можно определить, если предварительно измерить его стороны a, b, а затем вычислить по формуле A = a*b. Такой способ сопряжения физической величины х с числом Х получил название косвенного. Он возможен в том случае, если известна математическая связь между величинами, характеризующими вычисляемую величину.
Величины, которые сопрягаются с числом путем косвенных измерений, получили название вторичных. Разделение величин на первичные и вторичные условно. Например, такие величины, как длина, масса, время могут быть приняты за первичные. В этом случае сила – вторичная величина. Если в качестве первичных величин взять длину, время и силу, с которой тело притягивается к Земле, то масса становится вторичной величиной.
2. Вторичные величины выражаются через первичные с помощью, так называемых, определительных уравнений, которые составляются на основе физических законов, понятий, определений. Приведем примеры определительных уравнений.
Из геометрии известно, что объем параллелепипеда равен V = a*b*c, где a, b, c – стороны данной фигуры. Формулу можно представить в виде функции V = f(a, b, c). Скорость равномерного движения точки есть отношение пути ко времени v = l/t, её также можно представить как функцию v = v(l,t). Наконец в согласии с законом Ома напряжение U есть функция от силы тока I и сопротивления R: U = U(I;R). Примеры можно продолжать и далее, но уже очевидно, что вторичную величину «у» можно выразить как функцию первичных величин хi (i = 1,2,…, )
Y = f(x1, x2,…,xn) = y(xi). (7.4)
Метрология различает два вида определительных уравнений: уравнение связи между первичными и вторичными величинами и уравнения связи между численными значениями этих же величин. Первые (7.4) представляют собой функциональную зависимость от первичных величин, в общем виде, и независимо от ЕИ. Вторые уравнения отражают связь между численными значениями вторичной и первичных величин, полученными на основе уравнения (7.4). При этом очевидно, численные значения вторичной величины Y будут изменяться с изменением ЕИ первичных величин (см. выражения 7.2 и 7.3).
2. Положим, при выбранных ЕИ первичных величин х’oi, х’’oi численные значения этих величин X’i, X’’i равны согласно (7.1)
X’i = xi /х’oi; X’’i = xi /х’’oi, (i = 1,2, …, n) (7.1a)
Соотношения между X’i, X’’I найдем в соответствии с (7.2) и (7.3)
![]() (7.2а)
(7.2а)
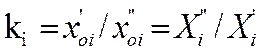
![]()
Подставляя (6.2а; 6.3а) в (6.4), получим
![]() ; (7.5а)
; (7.5а)
![]() (7.5б)
(7.5б)
Каким требованиям должно отвечать определительное уравнение и какова его структура?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.