Геометрические, кинематические и силовые параметры прямозубых конических передач. Расчет прямозубой конической передачи на контактную прочность. Назначение и классификация муфт

Лекция 8.

29. Геометрические, кинематические и силовые параметры прямозубых конических передач.

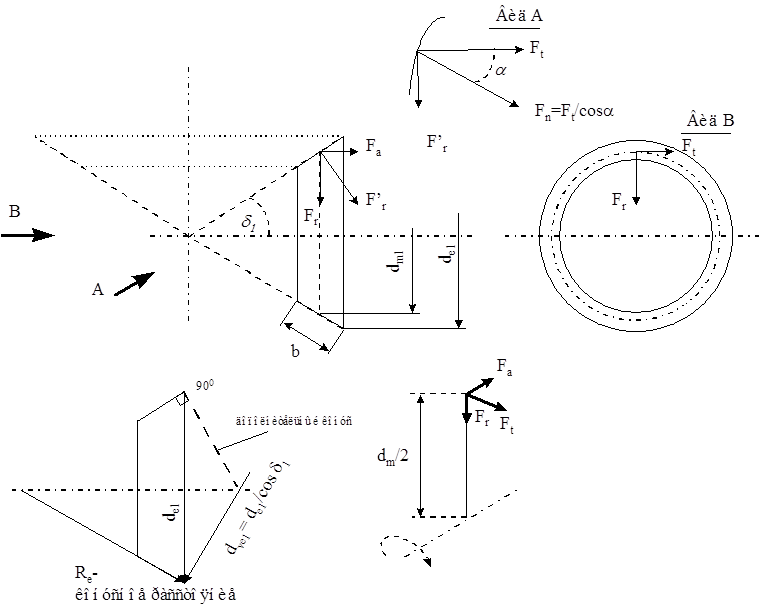
16. Расчет прямозубой конической передачи на контактную прочность.

По аналогии с обычным прямозубым зацеплением в цилиндрической передаче тангенциальная сила которая, собственно и осуществляет передачу крутящего момента

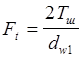                                                                                        (1);

является определяющей для всех остальных сил, которые определяются геометрией колеса. Сила контакта двух колёс всегда ортогональна поверхности в точке контакта, а её величина будет определяться силой F_t. Для выражения силы контакта колёс через тангенциальную силу необходимо определить текущее положение в пространстве контактной поверхности двух колёс, оно в свою очередь определяется:

- через геометрию эвольвентного профиля в сечении, нормальном образующей зуба - знакомая форма из прямозубого цилиндрического зацепления (лекция 3)

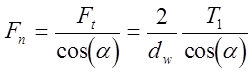,                                                           (2);

                                                                             

- смещением: для простоты принимаем что суммарное смещение колёс (лекция 4) равно 0 т.е. x₁=-x₂; поэтому здесь

a_w = a; d_w1=d₁                                                                                                                     (3);

- углом между зубом и образующей конуса: сама образующая зуба может совпадать с образующей этого показать конуса - прямозубое коническое зацепление, а может быть под углом - элементом спирали на конической поверхности показать косозубое коническое зацепление, при этом сила развернётся в плоскости касательной конусу, здесь для простоты принимаем прямозубое b=0,

- разложение силы на поверхности конуса, как функция угла конуса d, согласно рисунку

,                                          (4);

передаточное число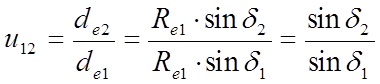 из рисунка для прямозубого зацепления Þ

отсюда получим передаточное число в конической передаче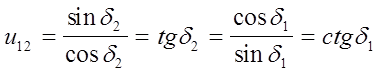                                               (5);

Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому.

Основные геометрические параметры конического колеса

Конусное расстояние - от вершины конуса до текущего диаметра

Дополнительные конусы - образованы нормалями к поверхности конуса

При пересечении торцевым сечением мы видим зуб соответствующий обычному прямозубому зацеплению с очевидным из рисунка соотношением

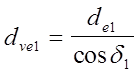                                                                               (6);

если мы возьмем окружность такого диаметра и распределим на ней зубья с тем же модулём на внутреннем торцевом сечении m_e то их число будет иметь значение (не целое)

z_v1=z₁/cosd₁                                                                                    (7);

теперь, приведя задачу к обычной прямозубой цилиндрической передаче, можем найти контактное напряжение в лекции 3 была приведена формула напряжения при соприкосновении двух цилиндров с модулем упругости  Е_пр, приведённого радиуса r_пр,

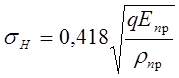                                                                         (8);

где:

                                                                                                   (9);

для эквивалентного цилиндрического колеса радиус кривизны поверхности зуба связан диаметром делительной окружности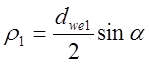, с учётом (6) кривизна

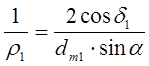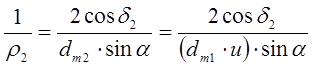;                        (10);

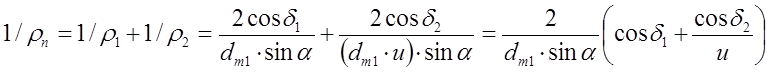(11);

из тригонометрии

;

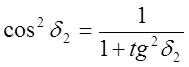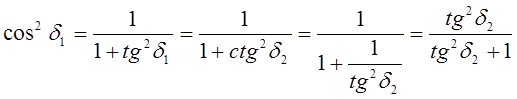
с учётом (5) 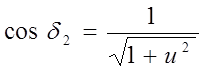;  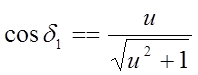           (12);

решая скобки в уравнении (10) получим

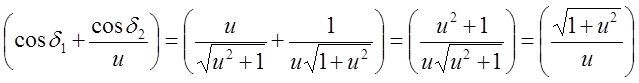                                                                                               (13);

окончательно получаем для приведённого радиуса кривизны

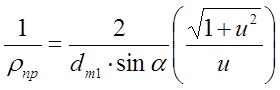                                                                                    (14);

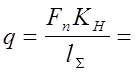 - удельная нагрузка                                                      (15);

l_S - суммарная длина контактных линий, в данном случае это просто длина одного зуба b_w

F_n как следует из рисунка 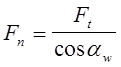                                       (16);

если сравнить полученные  и q с этими же величинами, полученными для прямозубого зацепления, мы увидим, что они отличаются только множителями   для конического против для прямозубого соответственно будет выглядеть итоговая формула для расчёта контактных напряжений для конического зацепления

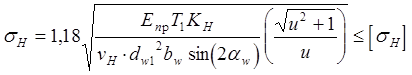                                  (17);

произведя замену 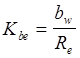 коэффициент ширины зубчатого венца,

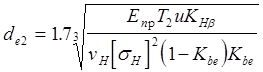
обычно в расчётах принимают K_be = 0.285

коэффициенты нагрузки K_Hv и K_Fv эмпирические определяются таблично по справочной литературе.

16. Расчет прямозубой конической передачи на изгибную прочность.

Из лекции 4 напряжение в опасном сечении, с поправкой на коническое колесо n_F  коэффициент эмпирический, для конических колёс имеет значение n_F = 0,85

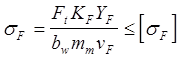
где: K_F  - коэффициент расчётной нагрузки, таблично из справочной литературы,

Y_F - коэффициент формы зуба, берётся из таблиц с заменой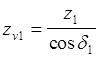

37. Назначение и классификация муфт.

Муфтами называют соединительные устройства для соединения концов валов, стержней, труб, электрических проводов и т.д.

Классификация по назначению (функционально):  

·управляемые - для включения и выключения рабочего (исполнительного) органа при непрерывно работающем двигателе;

·предохранительные - защищают от перегрузки(со срезаемым элементом);

·компенсирующие - несоосность и перекос;

·упругие - для уменьшения динамических нагрузок.

По рабочему телу:

·механические

·электрические

·гидравлические.

По управлению :

неуправляемые (постоянно действующие): глухие и компенсирующие;

управляемые: кулачковые и фрикционные;

самоуправляемые

38. Виды несоосности валов и их компенсация.

Продольное D_а

радиальное - эксцентриситет D_r

угловое D_a

для устранения несоосности применяют компенсирующие муфты, которые действуют либо за счёт движения жестких элементов либо за счёт упругих деформаций своих элементов