Винтовые конвейеры. Расчет валов на полную статическую прочность. Расчет валов на усталостную прочность

Рассчитываем подшипник на статическую грузоподъемность, проверим условие:

Р₀  С₀, где Р₀ – эквивалентная статическая нагрузка; С₀ – статическая грузоподъемность.

Для радиально-упорных шарикоподшипников:

Р₀ = Х₀ · F_r +Y₀· F_a = 0,5· 697,13+ 0,43·209,14 = 438,495 Н.

Х₀ = 0,5;    Y₀ = 0,43

С₀ = 3826 Н.

Р₀  С₀.

Расчет подшипников ведомого вала

 

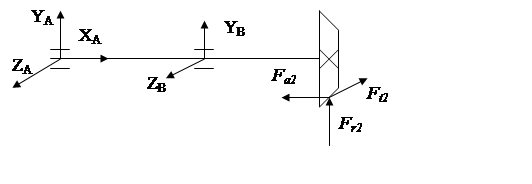Рис.15. Расчетная схема подшипников ведомого вала.

Y_A = 180,38 Н,         Y_В = 112,18 Н,

Z_A = 321,75 Н,          Z_В = 679,25 Н,

Х_A = F_a2 = 116,38 Н.

Находим суммарные реакции:

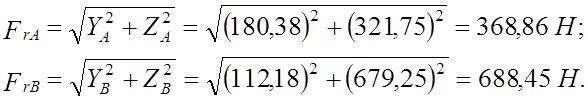
выбираем упорно-радиальный конический подшипник №7202 с углом контакта α =12 ⁰

S = 0,83e F_r;      где е – коэффициент осевого нагружения.

S_A = 0,83·0,45·368,86 =137,77 Н,

S_В = 0,83·0,45·688,45 = 257,14 Н.

S_А < S_В,   F_a2 ≤ S_В – S_А ,

F_aA = S_В - F_a2 = 257,14 - 116,38= 140,76 Н,

F_aВ = S_B = 257,14 Н.

Для подшипника А отношение

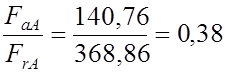< е, поэтому при расчете эквивалентной нагрузки не учитываем осевые силы.

Р = Х·V ·F_r ·К_б·К_т, где     Р – эквивалентная нагрузка;

Х = 1

V =1 при вращении внутреннего кольца,

К_б = 1,5 – коэффициент безопасности,

К_т = 1 – температурный коэффициент.

Р_А = 1·1·368,86·1,5·1 = 553,29 Н.

Для подшипника В  отношение

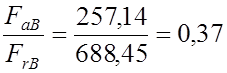< е, поэтому при расчете эквивалентной нагрузки осевые силы   не учитываем.

Р_В = Х·V·F_r·К_б·К_т,

Р_В = 1·1·688,45·1,5·1 = 1032,68 H.

Р_В>Р_А  , поэтому расчет ведем по  Р_В.

Проверяем условие:

0,6С > Р_В;   где С = 10,5 кН – динамическая грузоподъемность;

0,6·10,5·10³ = 6300 > 1032,68.

Рассчитываем долговечность подшипника:

;

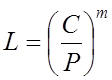где     L - долговечность подшипника в миллионах оборотов;

С - динамическая грузоподъемность;

Р – эквивалентная нагрузка;

m – показатель степени, для роликовых подшипников  m = 10/3.

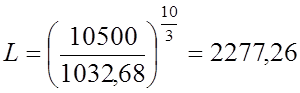млн. об.

Долговечность в часах:

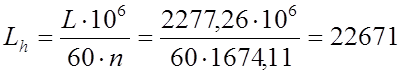 часов.

Рассчитываем подшипник на статическую грузоподъемность, проверим условие:

Р₀  С₀, где Р₀ – эквивалентная статическая нагрузка; С₀ – статическая грузоподъемность.

Для упорно-радиальных роликоподшипников:

Р₀ = F_a + 2,3·F_r·tgα = 257,14 + 2,3·688,45·tg12˚ = 593,71 Н.

С₀ = 6100 Н.

Р₀  С₀.

Выбор и расчет шпонок:

Шпонка проверяется на смятие.

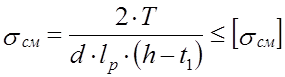,     [2, c.169-170]

где     Т – момент на валу;

d – диаметр вала в месте установки шпонки;

l_р – рабочая длина шпонки;

h – высота шпонки;

t₁ – глубина шпоночного паза.

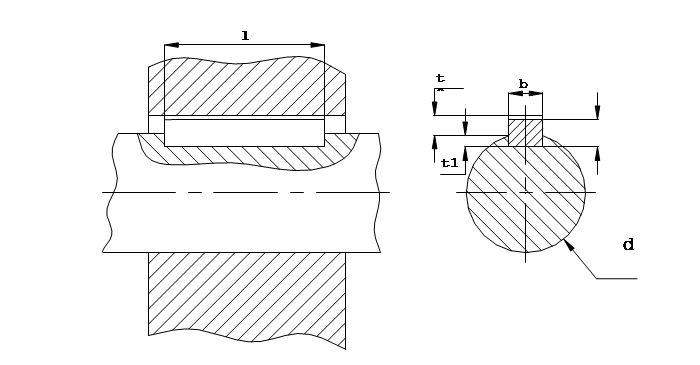
Рис. 16 Шпонка призматическая.

Расчет шпонок ведущего вала

Шпонка под цилиндрической шестерней:

Т = 4,96 Н·м,  d =15 мм,  b = 5 мм,  h = 5 мм,  t₁ =3 мм,  t₂ =2,3  мм.

l_р = l - b ,  где  l= 12 мм –длина шпонки

.

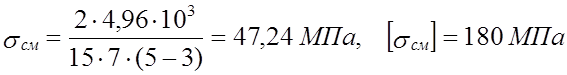σ_см < [σ_см],

Расчет шпонки входного конца вала:

Т = 4,96  Н·м, d =10  мм, b = 4 мм, h = 4 мм, t₁ =2,5 мм, t₂ =1,8 мм.

l_р = l - b , где     l =12 мм – длина шпонки;

l_р =12-4 =8 мм.

.

Расчет шпонок промежуточного вала

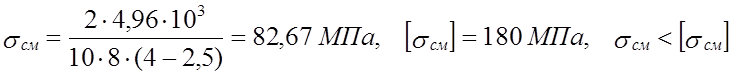Шпонка под цилиндрическим колесом:

Т = 7,7  Н·м, d =15  мм, b = 5 мм, h = 5  мм, t₁ =3 мм, t₂ =2,3 мм.

l_р = l - b , где     l = 8 мм – длина шпонки;

l_р =8 – 5 = 3 мм.

.

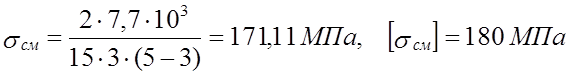σ_см < [σ_см],

Шпонка под конической шестерней:

Т = 7,7  Н·м, d =15  мм, b =5 мм, h = 5  мм, t₁ =3 мм, t₂ =2,3 мм.

l_р = l - b , где     l =12 мм – длина шпонки;

l_р =12 –5 =7 мм.

.

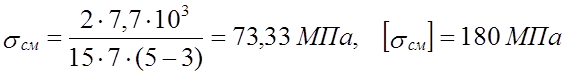σ_см < [σ_см],

Расчет шпонок выходного вала

Шпонка под коническим колесом:

Т =14,3  Н·м, d =18 мм, b = 6 мм, h = 6 мм, t₁ = 3,5 мм, t₂ = 2,8 мм.

l_р = l - b , где     l = 10мм – длина шпонки;

l_р =10 – 6 = 4 мм.

.

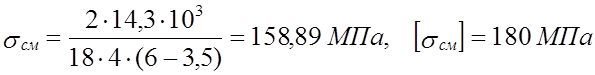σ_см < [σ_см],

Расчет шпонки выходного конца вала:

Т =14,3 Н·м, d =14  мм, b = 5 мм, h = 5 мм, t₁ = 3 мм, t₂ =2,3 мм.

l_р = l - b , где     l =16 мм – длина шпонки;

l_р =16 - 5 =11 мм.

.

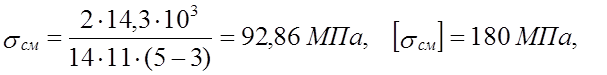σ_см < [σ_см],

Уточненный расчет валов:

Расчет валов на усталостную прочность

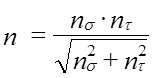< [n];

где     n – нормативный коэффициент запаса прочности, определяется для трех сечений: для наиболее опасного сечения, для выходного конца вала и для сечения максимальных концентраторов напряжений.

n_σ – коэффициент запаса прочности по нормальным напряжениям.

n_τ - коэффициент запаса прочности по касательным напряжениям.

[n] = 1,5 – допускаемый нормативный коэффициент запаса прочности.

;

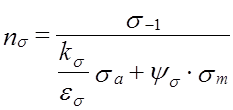где     σ_-1 = 0,43∙σ_в = 0,43∙900 = 387 МПа – предел выносливости стали при симметричном цикле;

k_σ – коэффициент концентрации нормальных напряжений;

ε_σ – масштабный фактор для нормальных напряжений;

σ_а – амплитуда цикла нормальных напряжений;

σ_m – средне напряжение цикла нормальных напряжений.

;

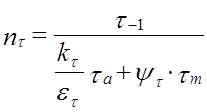где     τ_-1 = 0,58∙σ_-1 = 0,58∙387 = 224,46 МПа – предел выносливости стали при симметричном цикле;

k_τ – коэффициент концентрации касательных напряжений;

ε_τ – масштабный фактор для касательных напряжений;

τ_а – амплитуда цикла касательных напряжений;

τ_m – средне напряжение цикла касательных напряжений

Ведущий  вал

Наиболее опасное сечение и сечение наибольшего концентратора напряжения совпадают, поэтому расчет производим для двух сечений.

Для наиболее опасного сечения и сечения наибольшего концентратора напряжения.

Коэффициент запаса прочности по нормальным напряжениям:

k_σ = 1,9; ε_σ = 0,94; σ_а = 21,18 МПа; ψ_σ = 0,2; σ_m = 0.

 .

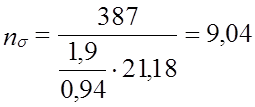Коэффициент запаса прочности по касательным напряжениям:

k_τ = 1,9; ε_τ = 0,86; τ_а = 7,49 МПа; ψ_τ = 0,1; τ_m = 0,5∙τ_а = 0,5∙7,49 =3,745 МПа.

;

.

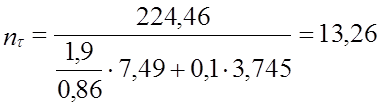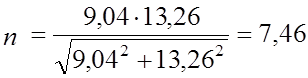n > [n].

Расчет входного конца.

Производим только по касательным напряжениям, так как нормальные напряжения отсутствуют.

Коэффициент запаса прочности по касательным напряжениям:

k_τ = 1,9; ε_τ = 0,92; τ_а = 50,06 МПа;  ψ_τ = 0,1; τ_m = 0,5∙τ_а = = 0,5∙50,06 = =25,03  МПа.

.

Расчет промежуточного вала на усталостную прочность

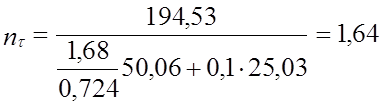Все три сечения, в которых нужно производить расчет совпадают.

Коэффициент запаса прочности по нормальным напряжениям:

k_σ = 1,79; ε_σ = 0,865; σ_а = 55,7 МПа; ψ_σ = 0,2;

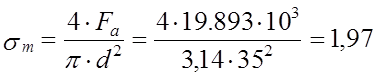 МПа.

.

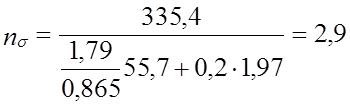Коэффициент запаса прочности по касательным напряжениям:

k_τ = 1,68; ε_τ = 0,75; τ_а = 30,12 МПа; ψ_τ = 0,1; τ_m = 0,5∙τ_а = 0,5∙5,22 =15,06 МПа.

;

.

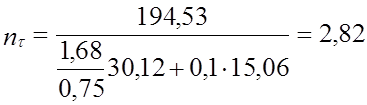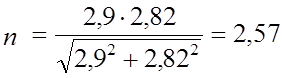n > [n].

Расчет выходного вала на усталостную прочность

Наиболее опасное сечение и сечение наибольшего концентратора напряжения совпадают, поэтому расчет производим для двух сечений.

Для наиболее опасного сечения и сечения наибольшего концентратора