Исследование RL-цепей и RС-цепей при синусоидальном источнике тока. Явление резонанса напряжений и резонанса тока в цепи синусоидального переменного тока. Исследование трансформатора, страница 4

Так как X_k = 2π f L_k, аX_c = 1/(2π f C), то при неизменной частоте в цепи переменного тока  fусловия,  в которых возникает резонанс напряжений, могут быть созданы или изменением индуктивности катушки L_k, или емкости конденсатора C. В данной работе условия резонанса создаются изменением индуктивности катушки за счет перемещения в ней стального сердечника. Первое измерение проводится при полностью введенном сердечнике в катушку индуктивности. В этом случае индуктивность катушки очень велика и Х_k будет больше Х_c.

После первого измерения сердечник следует медленно выдвинуть из катушки индуктивности. Так как индуктивность катушки L_k и ее реактивное сопротивление X_k при этом уменьшаются, а, X_c=const, то ток в цепи будет возрастать. Второе измерение следует проводить при значении тока в электрической цепи, близком к максимальному. Для этих двух измерений характерно преобладание индуктивного сопротивления  над емкостным (X_k>X_c), т.е. ток I₁отстает от напряжения в электрической цепи U₁на угол φ. Максимум тока в электрической цепи возникает при условии X_k=X_c тогда напряжение на конденсаторе и реактивная составляющая напряжения на катушке U_2p, находясь в противоположной фазе, компенсируют друг друга. Сдвиг по фазе между током и напряжением отсутствует, т.е.φ = 0 и cosφ =1. Такое явление называется  резонансом напряжений.

Полное сопротивление электрической цепи в этом случае будет:

Максимальное резонансное значение тока можно определить из соотношения I_рез = U₁ / R, где для любого измерения R= P/ I².

Четвертое и пятое измерение проводятся при значениях тока, когда он по достижении I_рез начинает уменьшаться. В этом случае индуктивность катушки такова, что ее реактивное сопротивление становиться меньше сопротивления конденсатора т.е. Х_k<X_cи в электрической цепи преобладает емкостное сопротивление, в связи с чем напряжение в ней U₁отстает от тока I на угол φ.

Векторные диаграммы во всех случаях следует строить следующим образом. По оси абсцисс следует направить вектор тока I, а вниз от него из его начала (по оси ординат) — вектор напряжения на конденсаторе U₃, отстающий от тока на угол φ = 90º. Из конца этого вектора вектором-радиусом, равным напряжению U₂, надо сделать засечку. Вторую засечку следует сделать из начала вектора U₃вектором-радиусом, равным напряжению в электрической цепи U₁. Точку пересечения засечек О следует соединить с началом и концом вектораU₃. Затем вектор напряжения U₂ надо разделить на два составляющих вектора:U_2aиU_2p, как показано на примерах векторных диаграмм, изображенных на рисунке 3.2.

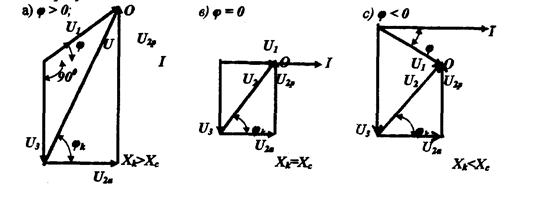
Рис. 3.2. Векторные диаграммы токов и напряжений для случаев:

а)>0;  в}=0; с) <0.

Значения U_2pи cos(φ) во всех случаях определяются из векторных диаграмм, построенных в соответствующем масштабе. Реактивное сопротивление катушки индуктивности для каждого измерения можно вычислить по формуле:

X_k = U_2p / I [Oм].

По результатам измерений и расчетов построить графики зависимостей U_2p=f₁(L_k) и U₃=f₂(L_k).

Лабораторная работа № 4.
Явление резонанса токов в цепи
синусоидального переменного тока

Цель работы:

Ознакомиться с физической сущностью явления резонанса токов в разветвленных цепях переменного тока.

Необходимое оборудование и приборы (шт.):

– вольтметр на 150+300 В…………………………………………..3шт.,

– амперметр на 2,5+5 А……………………………………………..1шт.,

– ваттметр на 2,5+5 А, до 300 В…………………………….………1шт.,

– катушка индуктивности (w=1200 витков) с сердечником..1комплект,

– батарея конденсаторов 0 - 58 мкФ………………………………..1шт.,

– реостат на 30 - 40 Ом……………………………………………….1шт.

Последовательность работы:

1.  Собрать электрическую цепь в соответствии со схемой, изображенной на рис. 4.1.

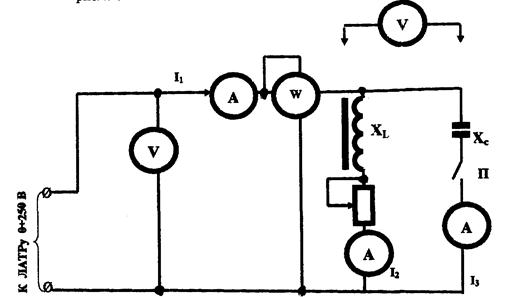
Рис.4.1. Схема исследования резонанса токов в цепи синусоидального  переменного тока

2.  Отключить конденсатор Си установить с помощью ЛАТРа ток I₁, равный 1,0 – 1,5 А, после чего произвести измерения.

3.  Установить емкость батареи конденсаторов  С = 58 мкФ и подобрать с помощью ЛАТРа ток I₁, равный 1,0–1,5 А, после чего произвести измерения.

4.  Установить среднее значение емкости батареи конденсаторов и подобрать с помощью ЛАТРа ток I₁, равный 1,0–1,5 А, после чего произвести измерения.

5.  Результаты измерений и вычислений внести в таблицу 4.1.

Таблица 4.1

6.  По результатам измерений и вычислений построить в выбранном масштабе векторные диаграммы.

7.  Определить емкость и реактивную мощность батарей конденсаторов для повышения коэффициента мощности от Cos(φ) до Cos(φ'). 

Методические указания:

Значительное влияние на эффективность работы энергетических систем оказывает коэффициент мощности сosφ = P/(U×I). Повышение сosφ может быть осуществлено с помощью статических конденсаторов. При выполнении данной лабораторной работы следует обратить внимание на то, что при отключенном конденсаторе во время первого измерения общий ток в цепи I₁равен току I₂, который равен сумме активной I_2аи реактивной I_2рсоставляющих (см. рис.4.2.).

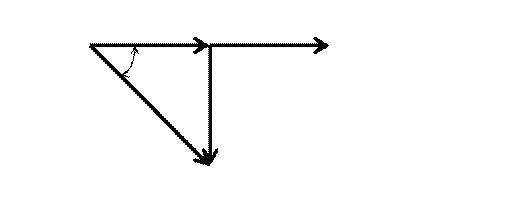
                          I_2а                  U

                        φ

                       I₁=I₂       I_2p

                                  O

Рис.4.2. Векторная диаграмма разложения вектора тока в цепи переменного тока

Во время второго и третьего измерений параллельно катушке индуктивности подключается батарея конденсаторов различной емкости С. Ток на конденсаторе I₃опережает напряжениеU на нем и находится в противоположной фазе с реактивной составляющей тока через катушку индуктивности, что приводит к взаимной (при резонансе полной, а в иных случаях частичной) компенсации. Следствием этого является уменьшение полного тока цепи при неизменном значении его активной составляющей и, соответственно, активной мощности Р (см.рис.4.3.).

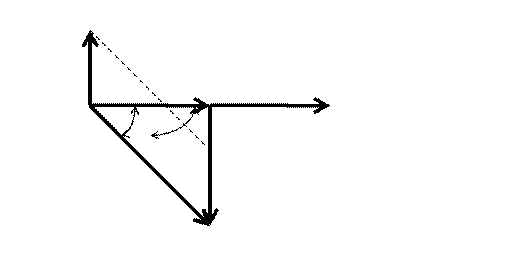
                               I₃