




ЛЕКЦИЯ 6
Стохастические регрессоры и инструментальные переменные
В практике статистических исследований и эконометрического моделирования очень часто довольно трудно определить, можно ли считать объясняющие переменные неслучайными. К тому же существует весьма широкий спектр реальных задач регрессионного анализа, в которых объясняющие переменные имеют явно стохастическую природу.
Разобьем описание регрессионного анализа линейных
моделей ![]() со стохастическими объясняющими
переменными на три случая:
со стохастическими объясняющими
переменными на три случая:
1)
объясняющие переменные независимы
от регрессионных остатков ![]() и их
распределение не зависит от оцениваемых параметров модели
и их
распределение не зависит от оцениваемых параметров модели ![]() и
и ![]() ;
;
2)
объясняющие переменные Х
коррелирован с регрессионными остатками ![]() ;
;
3) объясняющие переменные могут быть измерены только со случайными ошибками.
Природу
регрессионных остатков ![]() определим в
достаточно общем виде:
определим в
достаточно общем виде:
![]() ,
,
![]() .
.
1.
Случайные остатки не зависят от регрессоров ![]() и
оцениваемых коэффициентов регрессии
и
оцениваемых коэффициентов регрессии ![]() . В данном случае к нашей модели применимы все методы и
результаты, полученные при КЛММР (
. В данном случае к нашей модели применимы все методы и
результаты, полученные при КЛММР (![]() ) и ОЛММР (при
произвольной симметричной и положительно определенной матрице
) и ОЛММР (при
произвольной симметричной и положительно определенной матрице ![]() ). Правда, интерпретация этих
результатов при стохастических регрессорах
). Правда, интерпретация этих
результатов при стохастических регрессорах ![]() базируется
на понятии условного распределения регрессионных остатков
базируется
на понятии условного распределения регрессионных остатков ![]() , в котором в качестве условия
используется фиксированность матрицы
, в котором в качестве условия
используется фиксированность матрицы ![]() наблюдаемых значений
объясняющих переменных.
наблюдаемых значений
объясняющих переменных.
2.
Стохастические регрессоры Х
коррелированны. Если хотя бы одна из
объясняющих переменных Х асимптотически (по ![]() ) коррелирует
с регрессионными остатками
) коррелирует
с регрессионными остатками ![]() , то
, то ![]() не стремится (по вероятности) к нулевому
вектору и, следовательно, МНК- оценки
не стремится (по вероятности) к нулевому
вектору и, следовательно, МНК- оценки ![]() уже
не будут состоятельными. При этом всего один ненулевой элемент вектора
уже
не будут состоятельными. При этом всего один ненулевой элемент вектора ![]() может приводить к несостоятельности
всех компонент МНК- оценки
может приводить к несостоятельности
всех компонент МНК- оценки ![]() . Действительно,
. Действительно,
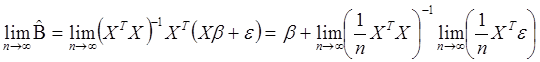 .
.
Мы видим, что корреляция между объясняющими переменными и регрессионными остатками является серьёзным препятствием к использованию обыкновенного метода наименьших квадратов. Поэтому для анализа моделей такого типа используется альтернативный метод, называемый методом инструментальных переменных.
В качестве основного инструмента метода используются
вспомогательные переменные ![]() , которые
требуется подобрать так, чтобы:
, которые
требуется подобрать так, чтобы:
1.
имелась бы принципиальная возможность измерять их значения на тех же объектах
(или в те же “моменты времени”), на которых мы располагаем значениями исходных
объясняющих переменных ![]() ;
;
2.
переменные ![]() должны быть асимптотически (по
должны быть асимптотически (по ![]() ) некоррелированы с регрессионными
остатками
) некоррелированы с регрессионными
остатками ![]() , т.е.
, т.е.
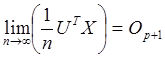 ;
(1)
;
(1)
3.
перекрестные (смешанные) вторые моменты переменных ![]() и
и
![]() в пределе (по
в пределе (по ![]() ) не все равны нулю и образуют
невырожденную (положительно определенную)
) не все равны нулю и образуют
невырожденную (положительно определенную) ![]() -матрицу
-матрицу
![]() , т.е.
, т.е.
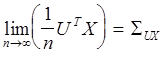 ; (2)
; (2)
4.
должна существовать положительно определенная матрица ![]() такая,
что
такая,
что
 .
(3)
.
(3)
Отметим, что если некоторые из исходных объясняющих
переменных ![]() можно считать некоррелированными с
регрессионными остатками
можно считать некоррелированными с
регрессионными остатками ![]() , то их можно
использовать для формирования столбцов матрицы
, то их можно
использовать для формирования столбцов матрицы ![]() и
находить дополнительно вспомогательные переменные только для оставшихся столбцов.
и
находить дополнительно вспомогательные переменные только для оставшихся столбцов.
Найденные в соответствии с условиями (1)-(4)
переменные ![]() называют инструментальными, а
оценки неизвестных параметров
называют инструментальными, а
оценки неизвестных параметров ![]() находятся по формуле
находятся по формуле
![]() .
(4)
.
(4)
Оценка ![]() будет
состоятельной, но, вообще говоря, не оптимальной. Оценка для ее условной
ковариационной матрицы
будет
состоятельной, но, вообще говоря, не оптимальной. Оценка для ее условной
ковариационной матрицы ![]() может быть
вычислена по формуле
может быть
вычислена по формуле
![]() ,
(5)
,
(5)
где
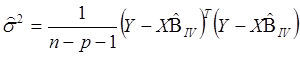 .
(6)
.
(6)
Анализ правой части (5) приводит к выводу, что чем
выше корреляция между ![]() и
и ![]() ,
тем точнее будут оценки метода инструментальных переменных
,
тем точнее будут оценки метода инструментальных переменных ![]() . И, наоборот, при слабой
коррелированности инструментальных переменных
. И, наоборот, при слабой
коррелированности инструментальных переменных ![]() с
исходными объясняющими переменными Х среднеквадратические ошибки оценок
оказываются чрезмерно большими, устремляясь в бесконечность при приближении
всех ковариаций между
с
исходными объясняющими переменными Х среднеквадратические ошибки оценок
оказываются чрезмерно большими, устремляясь в бесконечность при приближении
всех ковариаций между ![]() и
и ![]() к
нулевым значениям. Так, например, в случае единственной объясняющей переменной
к
нулевым значениям. Так, например, в случае единственной объясняющей переменной ![]() “инструментальная” оценка
коэффициента
“инструментальная” оценка
коэффициента ![]() наклона линии регрессии будет равна:
наклона линии регрессии будет равна:
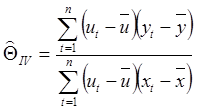 ,
,
а ее выборочная дисперсия
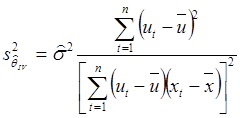 .
.
Так
что, если ![]() и
и ![]() слабо
коррелированы, то знаменатель в выражении для
слабо
коррелированы, то знаменатель в выражении для ![]() будет
близок к нулю и, следовательно, выборочная дисперсия оценки
будет
близок к нулю и, следовательно, выборочная дисперсия оценки ![]() окажется чрезмерно большой.
окажется чрезмерно большой.
3.
Случайные ошибки в измерении значений объясняющих переменных. Прежде всего отметим, что случайные ошибки в измерении
результирующего показателя ![]() (при условии их
нулевых средних значений и некоррелированности с объясняющими переменными
(при условии их
нулевых средних значений и некоррелированности с объясняющими переменными ![]() и регрессионными остатками
и регрессионными остатками ![]() ) приводят лишь к увеличению
остаточной дисперсии (или дисперсии остатка), но не влияют ни на несмещенность,
ни на состоятельность МНК- оценок. Действительно, пусть
) приводят лишь к увеличению
остаточной дисперсии (или дисперсии остатка), но не влияют ни на несмещенность,
ни на состоятельность МНК- оценок. Действительно, пусть ![]() -
вектор-столбец (высоты
-
вектор-столбец (высоты ![]() ) случайных ошибок измерения
анализируемого результирующего показателя
) случайных ошибок измерения
анализируемого результирующего показателя ![]() ,
так что в качестве его наблюденных значений мы располагаем вектор- столбцом
,
так что в качестве его наблюденных значений мы располагаем вектор- столбцом
![]() .
.
Получаем модель:
![]() .
.
Анализ (по стандартной схеме) полученных по
наблюдениям ![]() МНК- оценок
МНК- оценок
![]() ,
,
проведенный
с учетом свойств вектора случайных ошибок ![]() (
(![]() , подтверждает, что МНК- оценки остаются
несмещенными, состоятельными и оптимальными.
, подтверждает, что МНК- оценки остаются
несмещенными, состоятельными и оптимальными.
Теперь проанализируем , как влияют случайные ошибки в измерении значений объясняющих переменных на МНК- оценки параметров классической ЛММР. При этом мы будем предполагать:
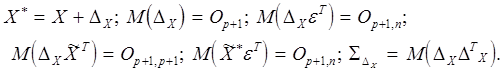
Здесь
![]() - вектор случайных ошибок в
измерении объясняющих переменных
- вектор случайных ошибок в
измерении объясняющих переменных ![]() -
-![]() -матрица искаженных наблюденных
значений объясняющих переменных, а
-матрица искаженных наблюденных
значений объясняющих переменных, а ![]() - вектор наблюдаемых
(искаженных) значений объясняющих переменных.
- вектор наблюдаемых
(искаженных) значений объясняющих переменных.
В рамках КЛММР получаем:
![]() .
.
МНК- оценка для ![]() будет
будет
![]()
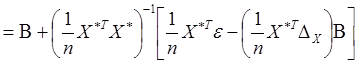 .
.
Проанализируем поведение правой
части при ![]() :
:
1) 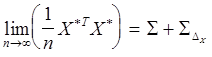 ; 2)
; 2) 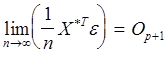 :
3)
:
3) 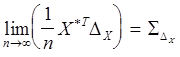 .
.
Переходя к пределу (по вероятности) при ![]() , имеем:
, имеем:
![]() .
(7)
.
(7)
Отсюда видно, что оценка ![]() в
данном случае не является ни состоятельной, ни несмещенной (ее асимптотически
неустранимое смещение оказывается равным величине
в
данном случае не является ни состоятельной, ни несмещенной (ее асимптотически
неустранимое смещение оказывается равным величине ![]() ).
Степень смещения оценки определяется истинным значением параметра, структурой
матрицы наблюденных значений объясняющих переменных и ковариационной матрицей
ошибок измерения.
).
Степень смещения оценки определяется истинным значением параметра, структурой
матрицы наблюденных значений объясняющих переменных и ковариационной матрицей
ошибок измерения.
Как же поступают при анализе подобных моделей? Это
зависит от априорной информации, которой располагает исследователь. Если из
предыстории или с помощью специальных экспертных опросов мы можем оценить
матрицы ![]() и
и ![]() ,
то на основании (7) можно построить “подправленную МНК- оценку”
,
то на основании (7) можно построить “подправленную МНК- оценку”
![]() .
.
В остальных случаях, как правило, обращаются к методу инструментальных переменных.
Тест Хаусмана
Как определить, следует ли
использовать инструментальные переменные или достаточно применять обычный метод
наименьших квадратов? Ответ на этот вопрос равносилен тестированию гипотезы ![]() против альтернативной гипотезы
против альтернативной гипотезы ![]() . Предположим, что наряду с обычной
МНК-оценкой
. Предположим, что наряду с обычной
МНК-оценкой ![]() есть оценка
есть оценка ![]() ,
полученная с помощью некоторых инструментальных переменных. При гипотезе
,
полученная с помощью некоторых инструментальных переменных. При гипотезе ![]() оценка
оценка ![]() является
состоятельной и эффективной, а при альтернативной гипотезе
является
состоятельной и эффективной, а при альтернативной гипотезе ![]() - несостоятельной. Оценка
- несостоятельной. Оценка ![]() состоятельна как при нулевой, так и
при альтернативной гипотезах. Таким образом, при нулевой гипотезе разность
состоятельна как при нулевой, так и
при альтернативной гипотезах. Таким образом, при нулевой гипотезе разность ![]() стремится к нулю, и естественно
ожидать, что при соответствующей нормировке распределение этой разности будет
асимптотически совпадать с каким-нибудь известным распределением.
стремится к нулю, и естественно
ожидать, что при соответствующей нормировке распределение этой разности будет
асимптотически совпадать с каким-нибудь известным распределением.
Хаусман (Hausman, 1978) доказал, что асимптотически
![]()
и величина
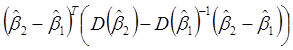
асимптотически имеет распределение хи-квадрат с ![]() степенями свободы.
степенями свободы.
Двухшаговый метод наименьших квадратов
Метод оценивания с помощью инструментальных переменных является обобщением обычного метода наименьших квадратов. Нахождение нужных инструментальных переменных является нелегкой задачей, решение которой зависит от конкретной ситуации.
Совпадение числа
инструментальных переменных с числом исходных переменных не является
обязательным условием. Достаточно потребовать, чтобы число инструментальных
переменных было не меньше, чем число независимых переменных. Выведем формулу
для ![]() в этом случае. Пусть
в этом случае. Пусть ![]() -
- ![]() -матрица,
столбцы которой линейно независимы, причем
-матрица,
столбцы которой линейно независимы, причем ![]() .
.
Воспользуемся геометрической
интерпретацией МНК. Рассмотрим каждый столбец ![]() ,
матрицы
,
матрицы ![]() как
как ![]() -мерный
вектор и спроектируем его на
-мерный
вектор и спроектируем его на ![]() -мерное
подпространство, порожденное столбцами матрицы
-мерное
подпространство, порожденное столбцами матрицы ![]() ,
получив векторы
,
получив векторы ![]() . Это эквивалентно тому,
что мы осуществляем регрессию
. Это эквивалентно тому,
что мы осуществляем регрессию ![]() на
на ![]() и находим прогнозные значения
и находим прогнозные значения ![]() . Их мы теперь будем считать новыми
независимыми переменными, и оценка
. Их мы теперь будем считать новыми
независимыми переменными, и оценка ![]() вектора параметров
вектора параметров
![]() строится с помощью обычной регрессии
строится с помощью обычной регрессии
![]() на
на ![]() .
Таким образом МНК применяется дважды – сначала для построения регрессоров
.
Таким образом МНК применяется дважды – сначала для построения регрессоров ![]() , а затем для нахождения оценки
, а затем для нахождения оценки ![]() . Эта процедура носит название двухшагового
метода наименьших квадратов.
. Эта процедура носит название двухшагового
метода наименьших квадратов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.