В соответствии с численными сомножителями для получения целого числа зубьев необходимо принимать р, кратное 4; принимаем р = 8 из условия получения z1 > 17 (при р = 4 не выполняется условие неподрезания для центрального колеса, так как z1 = 3·4 = 12 < 17).
z1 = 3×8 = 24; z2 = 6,75×8 = 54; z3 = 16,5×8 = 132; g = 52 (1 – 3n).
Проверки.
1) условие соосности — формула (9.1):
24 + 54 = 132 – 54; 78 = 78;
2) кинематическое условие — формула (9.3):
= 1 + 132/24 = 6,5;
3) условие соседства — формула (9.4):
(24 + 54) sin(180/3) – 54 = 13,55 > 2;
4) условие сборки выполняется, так как g — целое число при любых n (0, 1, 2 и т.д.); либо вторая проверка по формуле (9.7):
g = 
= 78 — целое число;
5) во внутреннем зацеплении интерференция отсутствует, так как z2 > 19, z3 > 81 в соответствии с табл. 9.1 (в зацеплении z2/z3 шестерней является колесо 2, а колесом — колесо 3).
Вывод. Все условия выполнены.
Величину КПД определяем по формуле:
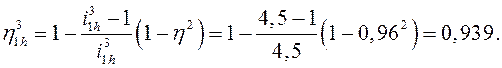(9.11)
В формуле (9.11) η – КПД одного зацепления.
9.3. Компьютерные расчёты
Оптимальные по габаритам размеры можно получить из компьютерных расчетов. Они позволяют рассчитать числа зубьев планетарного редуктора с любым передаточным отношением путем перебора чисел зубьев в задаваемых пределах от zmin до zmax. Основные принципы синтеза приведены в пп. 9.1 и 9.2.
1. Для редуктора Джеймса записывают условие соосности (9.1) в виде:
z1 + z2 = z3 – z2 = d, откуда числа зубьев
z1 = d – z2; (9.12)
z3 = d + z2. (9.13)
В формулах (9.12) и (9.13) d — аналог делительного межосевого расстояния;
а = 0,5m (z1 + z2) = 0,5md.
2. Из кинематического условия с учетом равенств (9.12) и (9.13) находят величину d:
= 1+ z3/z1
= 1 + (d + z2)/(d – z2), откуда
. (9.14)
3. Допускаемое отклонение передаточного отношения позволяет определить предельно допускаемые передаточные отношения:
, (9.15)
где Di — отклонение передаточного отношения.
После подстановки выражений (9.15) в формулу (9.14) получают значения dmin и dmax.
4. Организация циклов. В компьютерных расчетах внутренний цикл образуется изменением величины d, которая задается целыми числами в интервале dmin … dmax. По формулам (9.12) и (9.13) рассчитываются числа зубьев z1 и z3. При этом изменение чисел зубьев сателлитов z2 составляет внешний цикл.
5. Ограничения по числам зубьев осуществляют вводом zmin = = 17; zmax = 150 (или 200). Вначале принимают z2 = zmin. Компьютер рассчитывает числа зубьев z1 и z3 и проверяет условия z1 ³ zmin и z3 £ zmax. В дальнейшем величина z2 увеличивается на единицу. Пределом является z2 = zmax.
6. Проверку условий соседства, сборки и правильности зацепления выполняют в соответствии с п. 9.2.
7. Оптимизация по габаритам редуктора. Основной критерий оптимизации — минимальные габариты редуктора, связанные с числом зубьев корончатого колеса z3. В каждом цикле расчета записываются в памяти ПЭВМ числа зубьев z3 и заменяются только при выполнении условия
(z3) n < (z3) n-1.
После перебора чисел зубьев z2 в интервале zmin и zmax и выполнения всех условий числа зубьев z1, z2 и z3 выводятся на печать.
8. Для оптимального варианта рассчитывается механический КПД по формуле (9.7).
9. При составлении программы учтено, что при z1 = zmin = 17 и z2 = 19 (см. табл. 9.1) в соответствии с формулой (9.14) d ³ 36, поэтому варианты с d < 36 компьютер не рассматривает. Блок-схема алгоритма расчета чисел зубьев редуктора Джеймса приведена на рис. 9.4.
Пример 9.2. Рассчитать
на ПЭВМ числа зубьев z1, z2, z3
и КПД редуктора Джеймса (см. рис. 9.1) по исходным данным примера 9.1:
= 6,5; nс = 3; h = 0,96.
Решение.
По программе ТМ22 находим числа зубьев и КПД. Распечатка результатов расчета приведена на рис. 9.5.
Рис. 9.5
Вывод. Компьютерные расчеты дают меньшие габариты передачи, чем в примере 9.1 (z3 = 96 против 132). При этом обеспечена точность Di = 2,56 % при допуске в 4 %.
1. Чем отличается планетарный механизм от простого?
2. Назовите звенья планетарного механизма.
3. Для чего в планетарных механизмах принимают несколько сателлитов?
4. Как определяется передаточное отношение планетарного механизма?
5. Как определяется общее передаточное отношение двухступенчатого зубчатого механизма?
6. В чём заключается условие соосности планетарного механизма?
7. Как Вы понимаете условие соседства в планетарном механизме?
8. Что происходит при невыполнении условия сборки в планетарном механизме?
9. Как проверятся условие правильности внутреннего зацепления?
10. Содержание третьего листа курсового проекта
Лист формата А2 содержит синтез и анализ зубчатого механизма. В основной надписи листа делают запись типа: "Зубчатый механизм ДВС. Теоретический чертеж" и шифр: ТММ.М312.01.13.03 ТЧ. Лист выполняют в соответствии с разделами 8 и 9.
Синтез простого зубчатого механизма представлен картиной эвольвентного зацепления и блокирующим контуром для заданных чисел зубьев. На картине зацепления изображают 3…5 зубьев на каждом колесе, наносят геометрические и контрольные параметры в буквенных обозначениях. Анализ представлен диаграммами удельных скольжений и коэффициента давления. Синтез планетарной передачи представлен кинематической схемой сложного зубчатого механизма в двух проекциях, выполненной в масштабе.
Все изображения должны иметь заголовки и масштабы. На свободном поле листа показывают произвольно расположенную таблицу параметров с содержанием по п. 8.12. Образец листа 3 приведен на рис. 8.9.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.