Зубчатые передачи. Цилиндрические зубчатые передачи, страница 2

 = 8…15° - для косозубых колес;

 = 25…40° - для шевронных колес.

На развёртке можно отметить три шага: торцовый , нормальный  (расчётный) и осевой . Из соотношения между ними

                                                  (14.2)

находят соотношение между модулями:

                    ,   или     .                    (14.3)

Делительный диаметр находят через торцовый модуль:

.                                                 (14.4)

Размеры по высоте зуба переносятся со стандартного инструмента и определяются через нормальный модуль, который является расчётным (в этом случае индекс n опускается). Диаметры вершин и впадин:

;                       (14.5)

.                                               (14.6)

Межосевое расстояние:

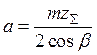.                                                    (14.7)

Формулы (14.4)… (14.7) универсальные, пригодные для косозубых и прямозубых колёс, где  = 0. Смещение режущего инструмента при нарезании косозубых колес, как правило, не выполняют.

14.2. Эквивалентные параметры

Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса. Нормальное к зубу сечение (рис. 14.2) образует эллипс с полуосями  и . Радиус кривизны эллипса в точке контакта:

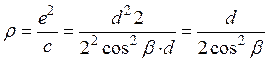.                              (14.8)

Диаметр эквивалентного прямозубого колеса (эквивалентный диаметр):

.                                        (14.9)

Эквивалентное число зубьев:

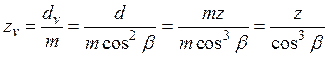.                       (14.10)

Из формул (14.9) и (14.10) следует, что эквивалентные параметры выше действительных. Вследствие наклона зубьев получается колесо как бы больших размеров, на котором нарезается большее число зубьев. Отсюда делают вывод, что косозубые колеса имеют большую прочность (больший ) и плавность хода (больший ), чем прямозубые.

Рис. 14.2. Эквивалентное колесо

NB 14.1. Так как эквивалентные параметры выше действительных, то косозубые колеса имеют большую прочность и плавность хода, чем прямозубые.

14.3. Геометрия зацепления

В цилиндрическом зацеплении точка контакта перемещается по линии зацепления В₁В₂ =, касательной к обеим основным окружностям. Практически зона контакта ограничена окружностями вершин колес, уменьшающих линию зацепления до активной линии зацепления А₁А₂ = . Так как колёса имеют рабочую ширину , то контакт происходит по контактной линии (точнее, контактной площадке), которая перемещается в поле зацепления (рис. 14.3) с размерами  и .

Рис. 14.3. Поля прямозубого и косозубого зацепления

В прямозубом зацеплении П (рис. 14.3) линия контакта 1 пары зубьев изображена в полюсе зацепления W. При вращении колёс линия 1 перемещается в поле зацепления и в тот момент, когда она займет положение 1', в зацепление войдет вторая пара с контактной линией 2'. На участках 1'–1'' и 2'–2'' работают 2 пары зубьев (заштрихованные участки). В точке А₁ зацепление первой пары прекращается, и на участке 2''–1' будет работать только одна (вторая) пара зубьев до положения 1', когда в зацепление войдет третья пара и т.д. Таким образом, в зацеплении практически находятся либо одна пара, либо две пары зубьев.