Другие предметы \ Детали машин

Планетарные передачи. Передача винт-гайка, страница 3

**      корончатого колеса .   .   .   .   .   .   .   .   .   .   .   .   .   .   .  65

** Передаточное отношение .   .   .   .   .   .   .   .   .   .   .   .   .   . 3,6

** Отклонение передаточного отношения .   .   .   .   .   .   .   .   1,408449Е-02

** КПД редуктора .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .    0,9433778

*******************************************************************************************

Рис. 19.12. Распечатка параметров редуктора Джеймса

Передаточное отношение:

Передаточное число u = z1/z2 = 25/20 = 1,25. Солнечное колесо  z1 – колесо с моментом Т1. Принимаем число сателлитов nc = 3. Приведенное число сателлитов  = 2,3. Расчётный момент Т2р = Т1 /  = 161,9·103/2,3 = 70,39·103 Н·м. Принимаем прямозубую передачу. Коэффициент ширины ψа = 0,25.

Принимаем 8-ю степень точности изготовления колёс. Коэффициент концентрации нагрузки КНβ = 1,1 [9] при несимметричном расположении колёс и твёрдости колеса Н2 < 350HB; коэффициент динамической нагрузки КНv = 1,05 [9] при скорости v < 5 м/с. Межосевое расстояние из расчёта внешнего зацепления z1/ z2 на выносливость по контактным напряжениям:

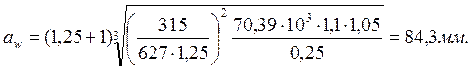
Модуль зацепления:

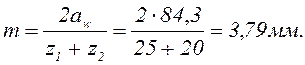
Принимаем m = 4 мм. Межосевое расстояние:

Ширина венцов колёс b = ψаaw = 0,25·90 = 22,5 мм. Принимаем b = 24 мм. Делительные диаметры: d1 = 4·25 = 100 мм, d2 = 4·20 = 80 мм, d3 = 4·65 = 260 мм. Окружная скорость колёс: v = π·100·646,7/60000 = 3,4 м/с. Коэффициенты нагрузки: КНβ = 1,15; КНv = 1,05; КFβ = 1,07; КFv = 1.4 [9]. Рабочее контактное напряжение внешнего зацепления:

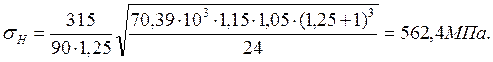
Во внутреннем зацеплении число зубьев шестерни  z2 = 20, колеса z3 = 65, передаточное число u = z3/z2 = 65/20 = 3,25. Передаточное отношение при остановленном водиле: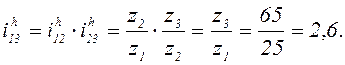   

Момент на корончатом колесе:

Т3 = Т1 · · = 161,9·103·2,6·0,962  = 387,9 ·103 Н·м.

Расчётный момент: Т2р = Т3 /  = 387,9·103/2,3 = 168,7·103 Н·м. Рабочее контактное напряжение внутреннего зацепления:

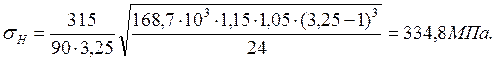
Вывод. Контактная прочность достаточна в обоих зацеплениях, так как рабочие контактные напряжения меньше допускаемого напряжения  = 627 МПа.

Окружное усилие в каждом зацеплении Ft = 2T1/(d1nc) = 2·161,9·103/(100·2,3) = 1408 Н. Коэффициенты формы зуба  YF1 = 3,9, YF2 = 4,09, YF3 = 4z3/(z3 + 20) = 4·65/(65 + 20) = 3,06.

         Рабочее изгибное напряжение зубьев солнечного колеса:

sF1 = YF1FtKFbKFn/(b1m) = 3,9·1408·1,07·1,4/(24·4) = 85,7 МПа.

Изгибное напряжение зубьев сателлитов:

sF2 = sF1YF2/YF1 = 85,7·4,09/3,9 = 89,9 МПа.

Изгибное напряжение зубьев корончатого колеса:

 sF3 = sF1YF3/ YF1 = 85,7·3,06/3,9 = 67,2 МПа.

Вывод. Изгибная прочность достаточна, так как рабочие изгибные напряжения меньше допускаемого напряжения  = 257 МПа.

Неуравновешенная сила, действующая на вал водила:

Fh = 0,2·2T1/(d1cosα) =0,2·2·161,9·103 /(100·cos20º) = 689 Н.

Сила, действующая на оси сателлитов:

F2h = 2Ft = 2·1408 = 2816 Н.

Частота вращения сателлитов:

Вопросы для самоподготовки

1.  Каковы достоинства и недостатки планетарных передач и области их применения?

2.  Чем обосновывается более высокая нагрузочная способность планетарных передач по сравнению с простыми?

3.  Назовите звенья планетарного механизма.

4.  Чем отличаются передаточное отношение и передаточное число в планетарной передаче?

5.  Какие принимаются конструктивные меры по выравниванию нагрузки по сателлитам?

6.  Каковы особенности расчёта планетарных передач по сравнению с простыми?

Вопросы, выносимые на экзамен

1.  Планетарные передачи. Оценка и применение. Кинематические схемы.

2.  Планетарные передачи. Силовые зависимости. Особенности расчёта на прочность.

Экзаменационная задача

Задача №38

Рассчитать межосевое расстояние и модуль простого планетарного редуктора. Вычертить кинематическую схему редуктора.

Скачать файл