Планетарные передачи. Передача винт-гайка, страница 2

          Неравномерность связана с тем, что каждое зацепление может находиться в разных стадиях (однопарном или двухпарном). Оказывают влияние также ошибки изготовления и монтажа. Кроме того, значение К_с зависит от конструкции редуктора. Так, если применить самоустанавливающиеся колёса, например, центральное колесо (рис. 19.10), то К_с = 1,1…1,2. При отсутствии компенсирующих устройств К_с = 1,2…2, и применение такой передачи даёт малый эффект. При плавающем центральном колесе рекомендуется при трёх сателлитах принимать приведенное число сателлитов = 2,3.

 

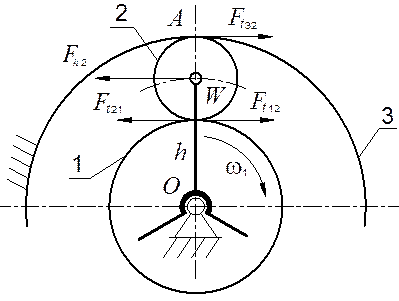    Рис. 19.9. Силы в зацеплениях          Рис. 19.10. Самоустанавливающееся

                                                                  солнечное колесо

          Радиальные и осевые нагрузки определяют так же, как в простых передачах. Из моментного уравнения одного сателлита находят силу давления на ось сателлита (рис. 19.11):

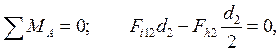   откуда                           

                                                     (19.2)

          Из уравнения проекций сил, действующих на сателлит, на ось Х находят:

 откуда                    (19.3)

 

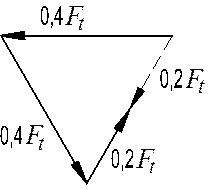Рис. 19.11. Треугольник сил в зацеплениях

          При расчёте валов следует исходить из допущения, что двумя сателлитами из трёх воспринимается по 40% нагрузки, а третий сателлит воспринимает 20% нагрузки (рис. 19.11). В результате остаётся 20-процентная неуравновешенность даже при постановке компенсирующих устройств. На вал водила при таких условиях будет действовать неуравновешенная сила

                                            (19.4)

Частота вращения вала водила                                                    (19.5)

Частота вращения сателлитов:

                                                 (19.6)

19.4. Расчёты на прочность

          Расчёт планетарной передачи ведут по формулам, выведенным для простой зубчатой передачи. Особенности расчёта.

          А) При одинаковых материалах всех колёс рассчитывают внешнее зацепление как менее прочное, по формуле:

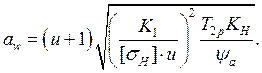                                             (19.5)

          Б) В формуле (19.5) используется передаточное число внешнего зацепления (но не передаточное отношение передачи), равное u = z₂/z₁ или u = z₁/z₂.

В) Расчётный момент определяют по формуле:

                                             (19.6)

   где Т₂  - крутящий момент на колесе (колесо – звено с большим числом зубьев).

Г) При разных материалах выполняют проверки обоих зацеплений:

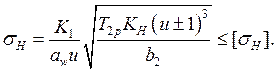                                 (19.7)

          Знак “минус” используется для внутреннего зацепления.

Д) Расчёт на изгиб ведут по формуле:

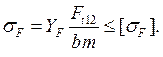                                        (19.8)

            Пример 19.1. Рассчитать планетарную передачу по следующим исходным данным: частоты вращения валов n₁ = 646,7 об/мин, n_h= 182,2 об/мин; крутящие моменты на валах Т₁ = 161,9 Н·м, Т_h = 551,8 Н·м, передаточное отношение   = 3,55. Допускаемое контактное напряжение  = 627 МПа. Допускаемое изгибное напряжение  = 257 МПа. КПД одного зацепления η = 0,96. Недостающими данными задаться.

Решение.

          Рассчитываем по программе ТМ12-7 в системе GWBASIC числа зубьев планетарного редуктора: z₁ = 25, z₂ = 20, z₃ = 65 (рис. 19.12).

*******************************************************************************************

******************************** РЕДУКТОР ДЖЕЙМСА *********************************

************** ****************************************************************************

** Число зубьев .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .**

**      солнечного колеса .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   25

**      сателлитов .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   20